CHAPTER 19 of The discovery of prime numbers formula and its results

CHAPTER 19

On the history of attempts for proving Fermat’s last theorem and the fundamental role of prime numbers
(regular) and its properties leading to solving Diophantine equation

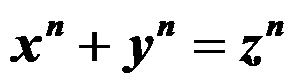
19.1. Diophantine equations

Generally, solving the Diophantine equations is one of the most difficult problems in mathematics and many special cases of them that have been solved, there is no general and decisive information except that limited cases. There is no Challenger in this area and if every one is interested in this subject, is welcome here. One of the most important kinds of Diophantine equations that have caused the motivation of human to a lot of new results is concerned to Fermat’s last theorem:

(1)

It is obvious that instead of investigating the equation (1) for every natural "n", it is enough to check equation (1) only for every prime number of "n", namely, because in case:

;

( p: prime number)

Here we express historical process of decisive proof of Fermat’s last theorem.

19.2. An introduction to the chronology of Fermat’s last theorem

When Pierre Fermat propounded his famous theorem in margin of Diophantus’s book in 350 years ago that equation hasn’t answer for integer number and and and claimed that he has an easy method for proving it (and since there was not enough space there, he ignored describing that). Many of greatest mathematicians have worked on it and if we ignore amateur persons who always have bothered the others, only a little improvement obtained about it. One of the basic advantages of Fermat’s last theorem was that the mathematicians solved very interior problems of mathematics specially in number theory, and new branches was made in this way that the most important of them are Algebraic numbers and geometry arithmetic. But, Fermat’s last theorem was not solved until in 1995 Andrew Wales presented a difficult solution for it in more than 200 pages.

Many of mathematicians became sorry of solving Fermat’s last theorem, because, Fermat’s last theorem was a motive for discovering a lot of properties of numbers. But we must wait for an easier solution for Fermat’s last theorem and from this aspect; mathematician's work is not finished.

We want to clarify the method in which the solution of Fermat’s last theorem is propounded by Wiles as it possible and in next part; we mention other possible solutions that are resulted from theorems of prime numbers like Wilson’s theorem, Fermat’s small theorem and theorem of "" function of Euler.

In fact, we want to show application of theorems about prime numbers in solving Diophantine equations and also we want to present some answers for solving general Diophantine equation:

(2)

In fact, we are going to verify and solve equation (2) that is an extension of equation (1) and it is really an extension of Fermat’s last theorem.

19.3. Chronology of Fermat’s last theorem

Pierre De Fermat (1608-1665), one of greatest mathematicians lived in 17^th century. He made bases of analytic geometry (almost contemporary with Descarte) and found a general method for searching maximum and minimum (that is completed to calculation of infinite similes). After all, the most famous results of Fermat are in the field of number theory.

Theorical-calculational results of Fermat were not printed. They were found in the letters and his scattered papers after his death.

Most of Fermat’s reasons for his results have not reached to us. These reasons and proofs have been arranged by mathematicians after him specially by Euler. Some of Fermat’s propositions clarifies that even himself had not a convincing reasoning for them. More over, it is clarified that some of his prepositions have error.

For example, Fermat’s guessed that every number in "" form is a prime number for every integer non-negative number "n", although Euler proved that this number is composite for "".

But in all of cases that Fermat claimed proof of a proposition, mathematicians could prove validity of proposition in some cases.

The most interesting and unique Fermat’s proposition is "Fermat's great theorem" or "Fermat’s last theorem". This theorem is:

When "n" be an integer number greater than "2", below equation:

can not have an answer for "x", "y" and "z" except "0". More over, we know that such numbers exist for. For example, 3, 4 and 5.In Fermat’s papers, proof of this theorem found for and it is interesting that this is the only perfect proof that has remained from Fermat.

But for general form and for "", Fermat has written in book margin of "Arithmetic" of Diophantus:

"In fact, "he" has found an interesting proof for it but the book margin is too small that it can be written in it".

Despite a lot of attempts of mathematicians, that as according to Dickson said, In his book "History of number theory" has engaged mathematicians for more than "350" years, this proof has not been obtained so that some people became doubtful about existing of such proof.

As we will see, except, for non values of "n", the validity of Fermat’s last theorem has not been proved by primary methods. Because of this, many of mathematicians attempted to prove that Fermat’s last theorem can not been proved by primary methods.

In 1908, Wolfskehl, a German who was interested in mathematics, put 100,000 marks prize for person that can solve Fermat’s last theorem. Immediately, hundreds and thousands persons who wanted the reward wrote a lot of letters to scientific organizations and publications that they could prove Fermat’s last theorem. Just in Guttingen of Germany, more than one thousand solutions were sent to mathematics society in Guttingen, "3" years after propounding Wolfskehl’s prize.

This illness had spread in all over Europe and even some people who had a little information about mathematics took part in this race. Every body presented their solutions that often were trivial and even funny that they had written them for the reward.

After the First World War that all over Europe encountered financial crisis, Wolfskehl’s prize lost its value and "FERMATISTS" lost their motivation of profit (Mathematicians had given this name to some people who attempted to solve the Fermat’s theorem with weak scientific possibility and useless method).

Because of this and naturally, the flood of "Fermatist’s proofs" subsided but not absolutely. Flow of letters to mathematics and scientific centers was still continued. The writers of these letters hoped to become famous at least, although even a little truth and correct reason had not been found in their letters. Some writers of these letters propounded that they didn’t attended to their personal honor but they wanted to do a useful work for science and this is an example of depravity and trifling in history of science.

Fermat’s last theorem was valuable for mathematicians specially because during the attempts to prove that, some new methods raised in mathematics and specially it helped and improved a branch of mathematics named "Algebraic number theory". This truth that Fermat’s theorem was unsolved means that, existence of new and exact methods is necessary in mathematics. It seems that the primary solution can not be found for Fermat’s theorem (it means that Fermat’s theorem can not be proved with known methods), But attempts to find the new methods for proving the Fermat’s theorem was valuable and useful for mathematics.

Apparently it is necessary to abandon searching for the primary solution for Fermat’s last theorem. Any way ether it is true or false, entering to primary solution of Fermat’s last theorem isn’t advisable specially for young and inexperienced mathematicians. One of the purposes of this chapter of the book is showing this point that Fermat’s theorem depends on how difficult and deep problems of number theory and how it has disappointed every body who had thought that he solved this theorem and put him among Fermatists (We ignore that in some cases, they didn’t find even deficit or later result).

It is better to remind that attempt to find a counterexample blindly is also disappointing.

In 1856, Harier Renrett reminded that if natural numbers, and exist that adapt in below equality:

They must adapt with below inequality [1]:

[2]

In fact, if we suppose that, then:

That it results:

With the same method, we can prove. Therefore:

It means and. Because of existing symmetry, it also results: and

We know that Fermat’s theorem is proved for every "n" smaller than 100,000 (1978). Therefore, for its examples, we must use numbers more than 10 ⁵⁰⁰⁰⁰⁰.

As we said, primary proof of Fermat’s last theorem doesn’t exist for none of numbers. Even in case "" that Euler verified it in 1768, it is clear that we must use numbers in below form:

(1)

("a" and "b" are integer numbers)

Fermat was unfamiliar with such numbers and it is clear that he couldn’t use them.

In fact, Euler’s proof has some defects, because he used numbers in form (1) without discussion about complex numbers and expressing their bases, and he considered the properties of integer number for them, for example, he has used the simplest rules of divisibly theory for integer number without proof for the numbers of (1).

The first person who arranged the calculus of numbers of (1) and made a certain base for Euler’s reasoning was Gauess apparently. In 1825, Dirichlet and Legendre proved Fermat’s theorem for "" almost contemporarily. Dirichlet’s proof was printed in 1828 that is very complicated. In 1921 Pelemelle simplified the proof to some extent.

For the next prime number, namely, Fermat’s theorem had been proved by Lame in 1839. Immediately after Lame, his proof became simple and complete by Lebesgue.

In 1847, Lame declared that he could prove Fermat’s theorem for all of prime numbers . Lame’s method was different from Euler’s cognition and it was based on arithmetic properties of numbers in below form:

(2)

That are integer numbers and "" is n-th root of number "1":

But Liouville found a serious deficit in Lame’s reasoning.

Deficit of this reasoning was that without reasoning Lame had supposed that numbers in form (2) are decomposed to multiple of prime factors uniquely like normal integer numbers. (That these factors aren’t decomposable to multiple of other factors). Lame had forced to accept his error.

As these events occurred in France, in Germany, a young mathematician, named Kummer was searching seriously about Fermat’s theorem. At first he thought that he could find the perfect proof of Fermat’s theorem and in 1843, send his letter to Dirichlet. This proof was based on such numbers in form (2) and Kummer repeated Lame’s error and supposed that these numbers are decomposed to prime factor only by one method. Dirichlet remembered immediately that this truth needs to proof and gave back Kummer’s letter to him.

Kummer found out soon that theorem about unique factorization to prime factors isn’t correct for numbers in form (2) and stopped his attempts to prove it. Kummer didn’t stop his searching and found an exit way that not only famed his name but also it led to a new branch in modern algebra. Kummer odd new numbers "abstract numbers" to numbers (2) and called them as "ideals" so that the property of being unique in decomposing to prime factors was correct.

We express an example. It is clear simply that in range of numbers in below form:

(3)

That "a" and "b" are integer numbers, number "21" is decomposed to multiple of prime factors by two methods:

Although numbers in form (3) aren’t numbers in form (2), for every value of "n" (for numbers (2), the same example is possible only for).

But we can use Kummer’s method about it. For this purpose, it is necessary to add "ideal numbers" A,B,C and D to numbers (3) and suppose:

It is clear that unique factorization is obtained for number "21" to multiple of prime factors (ideals).

Of course being "ideal" of new numbers has difficulties, but we can over come these difficulties. In 1847, Kummer could prove Fermat's theorem for all prime numbers that adapt with conditions named (A) and (B). As it is clear from Kummer’s letter to Liouville, Kummer thought that this condition is established for all prime numbers, but he found out soon that some exceptions exist (like number 37). Hilbert simplified Kummer’s proof in 1894.

But this conclusion of Kummer wasn’t favor, because he didn’t find even one prime number "" yet so that Fermat’s theorem is correct for it. Nevertheless, it was a basic point to improvement and we express it in more details.

In 1851, with hard and fine analyze, Kummer could complete seriously the results which he had obtained in 1847.He proved that condition (B) can be resulted from condition (A). (This proposition is famous as "Kummer’s pre-theorem").

And therefore, he simplified condition (A) as it was possible and the changed it that it can be used easily. This condition in its first arranging was with this request that prime number "" isn’t a divisor of "h" that was defined hardly. Kummer decomposed number "h" to multiple of two factors () and he obtained clear formulas for and ( that of course was diffidently ); Then he proved that number "h" is divisible by "" if and only if prime number "" doesn’t count form of the first number of Bernoulli , it means that it is not a divisor of them .(Of course with condition that these fraction aren’t reducible) . Kummer called such numbers as "regular"[3]. Bernoulli’s numbers are these rational numbers:

that they can be obtained respectively, according to a simple rule. Then, Kummer condition can be test for every "" without any special difficulty.

Specially it is cleared that only numbers: 37, 57 and 67 aren’t regular between prime numbers.

This improvement was very interesting that Kummer obtained it in completing his researches in 1847 but unfortunately proving these results is so hard that we can’t mention it here.

It is possible to show that why Bernoulli’s numbers exist with condition of being regular.

Kummer thought in all of his life that the number of regular numbers is infinite and a lot of mathematicians were agreeing with him in this field. But this truth has not been proved yet. Besides it, in 1915, Jensen proved with a simple method that conversely, the number of "irregular" prime numbers is infinite.

After 1851, Kummer attempted to search prime numbers that aren’t regular and tried to prove Fermat’s theorem for "irregular" prime numbers like for numbers 37, 59 and 67 hardly.

Therefore, validity of Fermat's theorem became proved for all of prime numbers. Although in years of first quarter of 20-th century Merteness and Vandiver found some lacks in Kummer’s reasoning but all of them can be reform easily. In 1893, Mirimanoff could prove Fermat’s theorem with easier method for power.

In 1850, France science academy put "3" thousand Frank prize for proving Fermat's theorem. Giving the reward had been retarded until in 1857, it was given to Kummer (apparently, at first, Kummer’s name wasn’t even among the candidates).

After Kummer, no serious work had been done for proving Fermat’s theorem till in 1929, Vandiver proved that Fermat's theorem is correct when prime powers of "":

I. Second factor "" from "h" isn’t divisible by "".

II. forms of Bernoulli’s term:

aren’t divisible by "" .

Testing the condition (2) isn’t difficult with modern computers. But for condition (1), although it has been tested about all of numbers, no prime numbers has been found yet for "" that it doesn’t adapt with this condition.

The condition (2) is also established for numbers. Therefore, Fermat’s theorem is correct for all prime numbers .

Euler knew that for verification below equation:

(4)

("" is a prime number greater than "3")

It is necessary to distinguish the case that none of numbers "", "y" or "z" aren’t divisible by "" from the one that at least one of these numbers is divisible by "".

If we have permission to a little carelessness, we can name this proposition that equation (4) can not be established for non–divisible numbers by "" as first case of Fermat’s theorem and call this proposition that equation (4) can not be established for numbers that one of them is divisible by "", as the second case of Fermat’s theorem.

Besides the general case of Fermat’s theorem, primary proof can be found about its first case for most of numbers "". Sophie Germain (1776-1831), the first woman mathematician of today worked on this problem at early 19-th century. She proved that the first case of Fermat’s theorem is correct for prime numbers "" if number "" be also a prime number.

In spite of these, Germain’s wish became hope less and the method which she selected to prove wasn’t useful even for the first case of Fermat’s theorem.

Germain didn’t print her results but wrote them in a letter to Lagendre, the French mathematician. In 1828 Lagendre published a detailed thesis about Fermat’s theorem and mentioned the Germain theorem in it and resulted from them a sequence of results. For example, he proved that the first case of Fermat’s theorem is correct for prime powers of "" when at least one of these five numbers is prime:

Besides it, the first case of Fermat’s theorem is correct for all of prime numbers smaller than 197.Lagendre’s theorem doesn’t respond for power 197.

After Lagendre, many mathematicians attempted to improve his results. Apparently, Venet, German mathematician obtained certain theorem in 1893. (This theorem can not be improved by primary method).

Venet considered an integer number with symbol "" for every and proved with general method of Germain that the first case of Fermat’s theorem is correct for every prime power of "" if exists then:

1. Number be a prime number and not divisible by ""

2. Number isn’t divisible by "p".

Number "" has three equivalent definitions:

I. with below assumption:

II. [4] is "resultant" of polynomial ""and "":

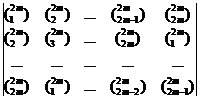
We remind that despite attempts of mathematicians that very clever and punctilious scientists were among them, no another primary method has been presented for proving Fermat’s theorem or at least for its first case.

(In spite of this, still Germain’s results aren't clear up to end. For example, still we don’t know that whether the number of prime powers of "" that these results use for them, is infinite or not).

Non-primary method for the first case of Fermat’s theorem was propounded by Kummer. He proved in 1858 that the first case of Fermat’s theorem for prime powers of "" is correct when at least one of these two Bernoulli’s number ( and ) isn’t divisible by "".

In 1905, Manov extended this result and proved that it is enough that one of the forms of four Bernoulli’s numbers isn’t divisible by "" and this includes all values of .

In 1909, Wieferich proved with use of Mirrimanov’s method that the first case of Fermat’s theorem is correct for all of prime powers of "" if isn’t divisible by "". This result is very interesting, because with help of it, for example we can judge about prime numbers smaller than or equal to "200183" except two numbers "1093" and "3511".

Laters, Mirrimanov and Frobenius simplified Wieferich’s proof that–Wieferich’s condition can be changed from base "2" to "3", so that the first case of Fermat’s theorem is correct for every prime power of "" that at least one of these two numbers or isn’t divisible by "".

In 1912, Furtwangler proved Wieferich and Mirrimanov- Frobenius’s criterion briefly and in some lines with a method famous as "bilateral rule" of Eisenstein.

This work was a start for a series of examinations for persons who obtained situation in the new field in number theory ( like about groups family) and they proved in 1941 that base "2" can be changed in Wieferich’s criterion with every prime number not greater than "43". This result could prove validity of first case of Fermat’s theorem for every powers of "" smaller than "253747889".

In 1934, Wandiver proved that the first case of Fermat’s theorem is correct for a prime power of "" that its second factor "", isn’t divisible by "". This theorem is interesting because as we said before, no prime power has been known till now that doesn’t adapt with this condition. But since "" isn’t divisible by "", researches are done only for with this method.

* ‌Here this question propound that how we can search about proof of Fermat’s last theorem?

At first, we remind, if three numbers (x, y and z) be integer numbers and adapt in below equation:

(1)

(we don’t put aside the case "" now), then every three numbers in () form adapt in this equation for arbitrary and integer number "". Conversely, if this triplet numbers () be an answer of equation (1), then is also answer of equation. Therefore, for finding all answers of equation (1) (except trifle case ), it is enough to calculate answers of so that "x", "y", "z" be coprime two-to-two (it means that they don’t have divisor except unit) and for proving that equation (1) hasn’t answer in set of integer numbers, it is enough to use counter demonstration and we suppose that answer of that includes numbers which are coprime to each other two-to-two , exists.

Moreover, it is clear that if in answer of from equation (1) two numbers from "x", "y" and "z" have a common factor like , without any doubt, the third number is also divisible by "". Therefore, in every equation in form (1), we can consider only one answer in form which "x", "y" and "z" are coprime two-to-two. We call such answer as "primitive answer". Then it is clear, if Fermat’s theorem is correct for a power like "n", it is also correct for every power in "an" form namely multiple of "n", because if below equation:

(2)

Has answer in set of integer numbers. Then, answer is obtained for equation (1). Therefore, it is enough to prove Fermat’s theorem for and (as we said before, Fermat himself proved this case "") that "" is a prime number greater than "2".

Here, we mention pretheorem that it has important effect in all reasoning about Fermat’s theorem.

20.2.1. Pretheorem

We suppose "a", "b" and "c" are natural numbers (namely integer and positive) so that:

1. Below equality be established:

2. Numbers "a" and "b" be coprime. Therefore, natural numbers "x" and "y" exist so that.

It means that if multiplication of two natural numbers that are coprime is equal to n-th power of a natural number, then every one of two factors of multiple is equal to n-th power of a natural number.

If "n" be an odd number. It is clear that this pretheorem is correct even for integer and non-zero (positive or negative) numbers "a", "b" and "c".

Proof. We express pretheorem completely. Suppose:

is factorization of numbers "a" and "b" to multiple of prime factors. Here , are different prime numbers, as the same method and are different prime numbers. More over, since "a" and "b" are coprime none of numbers of is equal with none of numbers of .

Therefore, below formula is decomposition of to multiple of powers of different prime numbers:

In other side we know (this is basic arithmetic theorem) that factorization of every natural number to multiplication of powers of different prime numbers is a unique factorization (if we don’t take in account the changing of factor’s row as two different factorization). It means that only with one method, we can obtain a natural number as multiple of powers of different prime numbers.

Therefore this factorization must be adapted with factorization of "c" when it has power "n" and it proves that all of powers are divisible by "n". Then "a" and "b" are equal with n-th power of a natural number.

We express this proof to emphasis on importance of basic arithmetic theorem (Is known for reader certainly).

For every primitive answer of below equation:

("" is a prime number and greater than "2") (3)

is equal with multiplication of two integer numbers:

And:

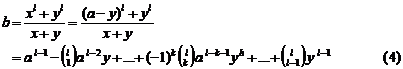
That is equal to:

Is coefficient of binomial extension (that sometimes is shown by symbol).

It is resulted from equality (4) that every common prime divisor "p" of "a" and "b" must be a divisor of below number:

And therefore if "", it is a divisor of . But when "p" be a divisor of "a" and , then it is a divisor of "" that it is impossible because according to the condition, and are coprime.

Now, if isn’t divisible by , then isn’t also divisible by , it means isn’t a divisor of "a" or "b". Therefore "a" and "b" are coprime and then according to pretheorem (for and ), there are integer numbers and , so that for them:

(5)

Now, attend that equation (3) can be written in below form:

Since in this equality numbers () have symmetric role, we can write the same equalities for three numbers and for the three numbers.

Therefore, for integer numbers,andthat are coprime and not divisible by "", more over they adapt in below equation("" is an add prime number):

(6)

Pairs of integer numbers and exist so that every two numbers of a pair are coprime and we have:

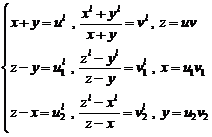(7)

These formulas are famous as "Abel formulas", although Germain knew them and Lagendre printed them for the first time.

We can obtain the same formulas (of course some complicated) for the case that one of numbers,and is divisible by "". But after 50 years researches about these formulas, no real formula has been found and so, we ignore to mention them here.

Guass propounded verification of theoretical – numeral problems about divisibility of numbers and easy and simple symbolization in this field.

We consider "n" as an arbitrary natural number. According to what Gauss said, "a" and "b" are congruent with module "n" when their subtraction "" is divisible by "n". So:

It is clear that congruence relation is an equivalent relation and therefore, set of all integer numbers can be divided to groups of congruent numbers. We show the set of these groups with symbol.

Congruencies can be added or multiplied to each other like equalities. Also we can simplify the congruence to its common factor if this factor and "n" be coprime.

We know that below congruence is established for every integer number "a" that is not divisible by"":

(8)

This proposition is called Fermat’s small theorem.

If we multiply congruence (8) in "a":

(9)

It is clear that this congruence is also established for . Therefore, congruence (9) is established for every integer number "a" and Euler arranged Fermat’s small theorem as this method.

In Algebraic language congruence (9) means that every member of field is a binomial root of "".

Congruence (9) can be proved without using theory of groups and with the same method.

Since prime number "" aliquots number "" (namely "" is divisible by "") and since doesn’t aliquot , so all coefficients of binomials:

are divisible by "". Therefore, for every two integer numbers "x₁ "and"":

The same result exists for every polynomial by using mathematics induction method:

(10)

If in this formula , formula (9) is obtained (for ) .

Now, we can propound Germain’s researches directly. We suppose as a primitive answer from equation (3) includes numbers not divisible by "". We choose arbitrary prime number "p" that is congruent in relative to module "" with unit, namely in below form:

That "m" is an integer number. We suppose none of, and are divisible by "p". Since, therefore an integer number like "" exists so: [5]

If we multiply equality (3) in and change it as congruence, it is obtained:

That and aren't divisible by "p".

We call integer number "as degree of "" in relative to module "p" if a number like "" not be congruence with "0" to module "p" exists so:

More over, we call two numbers "" and ""from "" degree as neighbor in relative to module "p", when:

The congruence that we proved above, according to this naming means that if no one of , and are divisible by "p", then neighborhoods from "" degree will exists in relative to module "p".

Now, we suppose that one of numbers, and are divisible by "p" (and according to primality of these numbers only one of them). For clarifying the situation, we suppose to be divisible by "p". Then one (and only one) of factors in Abel formula (see relation 7) namely and that are coprime is divisible by "p".

Suppose is divisible by "p". So isn’t divisible by "p" then:

In other word, it is resulted from formulas (7) of Able:

Therefore:

;

Therefore, if "" not be congruence with "0" to module "p", then again same neighborhoods of "" degree exist in relative to module "p". At last, suppose is divisible by "p". So in relation (4) (that), all terms of right side

except the last term , are divisible by "p" and therefore, we have:

but according to Abel's formula:

;

That "" is a number that for it:

(It is clear that or isn’t divisible by "p").

Therefore, it is proved that number "l" is from degree "l" for in relative to module "p".

Validity of below theorem also is proved.

19.4. Sophie Germain’s theorem

Suppose that an integer number like "m" exists for prime number so that

1. is a prime number

2. There isn’t any neighborhood between numbers from degree "" in relative to module "p".

3. Number "" is not from degree "" in relative to module "p". Then, for power "", the first case of Fermat’s theorem is correct. For testing the specific cases of conditions (2) and (3) of this theorem, it should be noted that below congruence is established for every "" with degree "" in relative to module "":

(11)

In fact, if that "" is not congruence with "0" to module "p", then according to Fermat’s small theorem:

19.4.1. Problem

Prove the inverse of this theorem. Every answer of "" from congruence (11) is from degree -th in relative to module "p".

It seems easily that for every prime number "p", only two unequal numbers exist for "" that adapt in below congruence:

So:

"1" and ""

It is clear that "1" and "" adapt in this congruence, but this point that this congruence hasn’t another root can be proved based on an Algebraic theorem. A polynomial of degree "n" can not have more than "n" root in one field. Also we can use from this point that below number is divisible by prime number "p" only when that "" or "" is divisible by "p":

Because numbers "1" and "" aren’t neighbor of -th degree in relative to module , clearly, it is resulted that condition (2) from Germain’s theorem is established for "" certainly.

Since can not be divisible by prime number, therefore condition (3) is established for"".

Then, if power "" (that is an add prime number) has this property that number "" is prime also then the first case of Fermat’s theorem is correct for "".

We know Germain obtained this result by her self (A lot of writers called it as Germain’s theorem).

Therefore, Germain’s general theorem resulted in Lagendre’s theorem. Remind that Lagendre’s theorem says that for prime power "" if "" is a prime number that "m" is one of five numbers "2,4,5,7 or 8" then the first case of Fermat’s theorem is correct.

Here, we prove it only for "" because with growing "m", induction becomes difficult.

Suppose that condition (1) from Germain’s theorem is established for "". Namely number "" is a prime number.

We test that condition (2) from this theorem is also established.

According to what we said before, we prove that there isn’t any neighborhood between roots of below congruence:

(12)

Since, then roots of congruence (12) are roots of two below congruencies:

We know that the first congruence has two roots, "1" and "". The second congruence has two cases. It hasn’t root or has two roots exactly:

and

In the first case, congruence (12) has two roots "1" and "" that they aren’t neighbor clearly. Then condition (2) from Germain’s theorem is established. In second case, congruence (12) has "4" roots:

Two roots of them can be neighbor only for:

If , then is divisible by that it is impossible for . And if , then:

Is divisible by, it means is divisible by that again it isn’t possible for . Therefore, condition (2) from Germain’s theorem is also established in the second case.

Now, we test the condition (3). If this condition is not established, then namely that it is resulted:

It means is divisible by "p".

Because we know "", it is possible only for "" but equation "" has answer "" that isn’t a prime number and then this case is also impossible. It means that the condition (3) of Germain’s theorem is also established.

19.4.2. Remark

Vent’s theorem led to Germain’s theorem. We must only prove that if prime number in "" form doesn’t aliquot Vent’s number namely"". Then condition (3) from Germain’s theorem is established.

19.5. Fermat’s last theorem for exponent "4"

Only the case "" from Fermat’s last theorem is proved by a primitive method. As we said before, Fermat found this proof by himself. He used formulas of general answer of below equation:

(1)

Indian mathematicians also knew these formulas. Here, we start from proving these formulas. We know that for equation (1) it is enough to find its primitive answers. It is clear that if is an answer of equation (1) and then is also its answer. In other side, for every answer of (x, y, z), at least one of or is even. In fact, if both of and are odd, then "" is in "" form that it can’t be equal to second power of an integer number (because all of second power, "", are in "" or "" form). Also it is clear that besides answer, () is also an answer of equation.

According to this points it is resulted that it is enough to find a primitive answer from equation (1) so that all of three numbers,, and are positive and be even.

Pretheorem. For every two positive and integer numbers "m" and that are coprime, with this thesis that one of "m" and "n" is even and another one odd, below formulas include three positive integer numbers that is a primitive answer of equation with condition of being even of :

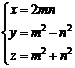(2)

Conversely, every three positive integer numbersare a primitive answer of equation (1) with thesis of being even of number, it can be expressed as form of formulas (2) that "m" and "" are coprime and one of them is even and another one is odd.

Proof. Below identity:

Show that numbers (2) (that are positive numbers clearly) are an answer of equation (1) that more over, is an even number. If these numbers have a common divisor like , then below numbers must be divisible by :

It means "" because according to the thesis "m" and "n" are coprime, but if "", then number ""is even. So, and are even or both of them are odd that it is impossible, because according to the thesis, one of "m" and "n" must be even and another one must be add, And this proves that answer (2) is a primitive answer.

Conversely, we suppose that is a primitive answer includes positive numbers and more over, even number"". Since and are odd, therefore, "" and "" are even. Suppose:

That and are positive clearly. Every common divisor of and will be also a divisor of "" and ". Therefore "", it means that and are coprime. In other side:

;

Therefore, according to the pretheorem, positive numbers "m" and "n" (that clearly are coprime and one of them is odd and another one is even) exist so that:

Then "" it means "" and so:

, ,

For completing the proof, it is enough to attend that"".Proving of the pretheorem finished.

Now, we can prove Fermat’s last theorem for"". We prove validity of the general proposition.

19.5.1. Theorem.

Below equation hasn’t non-zero answer in set of integer numbers.

(3)

Proof. We use contradiction for proving so we suppose that for equation (3), a non-zero answer exist in set of integer numbers. It is clear that without any disorder to generality, we can consider this answer as it contains the positive numbers that are coprime two-to-two. Since in every set of positive integer numbers, there is the smallest number, therefore, among these answers for equation (3), answer exists so that is the least possible value. We attend to this answer more.

As we proved for answer of equation (1), one of and must be even, here, we suppose that is an even number. It is clear that this assumption makes no disorder in the generality. Because:

(3)

Since numbers and and are positive and coprime two-to-two, and is an even number, therefore, according to the pretheorem two coprime numbers "m" and "" exist that one of them is even and another one is odd so that:

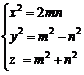
If "" and "", then:

that it is impossible, because, as we know the second power of every odd number must be in "" form. Therefore, "m" is odd and "n" is even. We suppose""and"", so:

Because numbers "m" and "" are coprime, it results:

in which "" and "t" are positive integer numbers and coprime.

Specially we see:

So:

Since "t" and "" are coprime, again we can use pretheorem for this equality.

Therefore, two coprime numbers "a" and "" exist that one of them is odd and another one is even so:

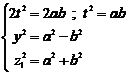
Because "a" and "b" are coprime. It is resulted from the first equality (according to the pretheorem) two integer numbers "" and "" exit so that for them:

Therefore, the third equality can be written below form:

and it means that is primitive answer from equation (3) that includes positive numbers. So, according to the answer, we must have:

So:

that below meaningless inequality is resulted:

Therefore, the assumption of existing answer for equation (3) makes paradox. It means that this equality doesn’t have any non- zero answer in set of integer numbers.

19.6. Fermat’s last theorem for exponent "3"

We said before that in 1768, Euler proved Fermat’s last theorem for case "" for the first time. Here, we reconstruct this proof. Euler expressed this pretheorem at the beginning.

Pretheorem. If two number "a" and "b" that are coprime, have this property that the number "" is the third power of an integer number, then two integer number "s" and "t" will exist so that:

At first we explain that how we can use this pretheorem for proving Fermat’s last theorem.

We suppose that Fermat’s last theorem doesn't be correct for "", it means integer numbers like, and exist so that:

(1)

We know that numbers, and can be considered coprime two-to-two. Then, only one of these three numbers can be even. In other side, it is clear that all of three numbers can not be odd (because sum or subtraction of two odd numbers is an even number). Therefore, one and only one of, and is even. Without any disorder to the generality can be considered as an even number. In fact, if be an even number, we can change the role of with, if be even we can change role of with by changing the sign because:

Between all of integer numbers and triplet that adapt in equation (1), with assumption to be even, it is possible to choose it so that has minimum possible value. Such minimum triplet numbers exist because in every set of positive integer numbers, the smallest number exists.

Since and are odd, therefore, below numbers are integer numbers:

Since:

(2)

Therefore, one of numbers "p" and "q" is even and another one is odd. More over these numbers are coprime clearly.

According to (1) and (2):

If we suppose"":

(3)

Since, one of two numbers "p" and "q" is even and another one is odd, "" will be an odd number. So, it is resulted from that "q" is divisible by "4" (it means "q" is an even number and "p" is an odd number).

According to pretheorem, multiplication of two numbers that are coprime, can be a third power of an integer number if and only if every one of them be third power of an integer number. In other side, numbers "" and"" are coprime only when numbers "q" and "" be coprime and it is possible if and only if every ("p" and "q" are coprime) "q" isn’t divisible by "3". So, if we suppose that "q" isn’t divisible by "3", then it is resulted from (3) that every one of numbers "" and "" is a third power of an integer number.

But, according to pretheorem, if "" be a third power of an integer number, then:

That "s" and "t" are integer numbers. Because "p" is odd, so, from equality "", it results that "t" is odd and "s" is even, in other side, because "p" and "q" are coprime, "t" and "s" also will be coprime. Since is a third power of an integer number, therefore:

also must be equal to the third power of an integer number. This proves that below number is also third power of an integer number:

Numbers "", "" and "" are coprime. In fact, if "" and "" have common prime divisor "", then "", because "" is an odd number.

Therefore "" must be common divisor of "s" and "", but since "t" and "s" are coprime, it is possible only for "". So, if numbers "" and "" have common prime factor "", then "", because both of them are odd numbers.

More over, below numbers are divisible by "":

That again it is possible only for"". Therefore, in both of two cases, number "s" and then number "q", will be divisible by "" in spite of the assumption. Since multiplication of numbers "", "" and "" that are coprime, two-to-two, is the third power of integer number. Therefore, every one of them must be third power of an integer number. It means that three integer numbers "", "" and "" exist so that

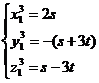
Then:

So, with start from three numbers, we can obtain three new numbers that adapt in equation (1) and more over have this property that their first number namely "", is even number. Since "" therefore . Because we have "", so and then:

So that it is paradox to the assumption of minimal of triplet numbers .

This paradox proves that number "q" must be divisible by "3":

that "r" is an integer number (and divisible by "4"). So, according to (3):

(4)

If integer numbers and "" be divisible by a prime number like "", then "", because if it isn’t so, then number "p" become divisible by "", it means that it has a common divisor with "q". But if "", then below numbers:

Namely "p" and "q" must be divisible by "" that is impossible. Therefore, numbers and "" are coprime.

So, it is resulted from (4) that both of these two numbers are the third power of an integer number and so, according to the pretheorem (if we use it about ""), below equalities are resulted:

(5)

That "s" and "t" are integer and coprime. More over, it is clear that "t" is even (because "r" is even) and then "s" will be odd. In other side, below integer number is equal to the third power of an integer number:

Since numbers "s" and "t" are coprime and more over, one of them is even and another is odd. Therefore, number, and are coprime two-to-two. So, every one of them is third power of an integer number so that integer numbers "", "" and "" exist:

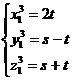
But in this situation we will have:

And also:

[1] . Because we have

[3]. Set of regular numbers are defined by formula of prime numbers. For more information refer to appendixes I (21.3).

[4]. For calculating determinant, refer to "H.M" new method that is written in end of book in appendixes I (21.2)

[5]. For avoiding the answer of general equation, refer to (H.M) table method in appendixes (21.1) at the end of this book.