CHAPTER 6

 

On the history of the problem of searching for finding generating function of prime numbers "p (n)"

6.1. A summery of the history of "2000" years old attempts for finding a formula for prime numbers

One of the first propounded subjects is that the number of prime numbers is finite or infinite?

Euclid, first time answered this question (more than 2000 years ago) and he proved by a kind of mathematical reasoning (ad absurdum statement), that the number of prime numbers is infinite. After that time mathematicians tried to find simple arithmetical formulas, so that with help of them, it is possible to find only prime numbers even if these formulas couldn’t present all of prime numbers. Fermat had a famous guess about it (that it didn’t express as a final conclusion) and that guess is that all of numbers in form of  are prime number. This guess is correct for n=0,1,2,3,4 and called these numbers as "Fermat prime numbers". In 1732, Euler could decompose F (5) to below form:

Therefore, it is proved that F (5) isn’t prime number. Later Euler could proverb that a lot of these numbers are decomposable and so composite. It is necessary to mention that so deep methods need to factorization these numbers in every special case. And because of greatness of these numbers, it has a lot of unsolvable difficulties. Till now, it couldn’t be proved that some of other Fermat’s numbers are prime number for.

Another simple and interesting function that generating the number of prime numbers is Euler’s function[1]:

In fact,  generating prime numbers for n=1, 2, 3, ..., 40 although, for   that isn’t a prime number, because:

Another function that generates prime number for n=1, 2, 3, …, 79 is:

This generator function of prime numbers also, for n=80, will encounter failure.

"In fact, searching simple expressions that generating just prime numbers is a useless work and even more useless would be trying to find a algebraic formula that generating "all" prime numbers (Richard Courant)."

 From Euclid time till now, human has desired a formula that generating just prime numbers. At first they thought that a polynomial like F(x) with correct coefficients exists that when an integer number is put instead of "n", prime number is obtained. But they found out soon that if  be prime then is divisible by "p" for every correct "k".

In other word it is proved that such function doesn’t exist and "F" can’t generate just prime numbers. After human became disappointed from polynomial, he tests non–polynomial formulas.

About this subject, in page "5" of famous book "An entrance on number theory" by Hardy and Wright which printed in 1945, is written:

"Of course must remember that a natural question become an erroneous question after discussion and verifying …. Is there any general formula for n^th prime number of? .... Answer of this question is that although it is acceptable as a natural question but generally it is erroneous then printed in 1968:

Is there any general formula for n^th prime number of""? … We don’t know such formula … possibility of such formula, is impossible certainly."

Therefore problems like what were said and especially inquiry about different forms of numbers for solve the problem of finding prime numbers formula, were subjects of researches of mathematicians. About this problem, we can name numbers in "" form that famous numbers of them are Fermat’s prime numbers  and Mersenne’s prime numbers (M_p=2^p-1) and they found favorite. About prime numbers formula, Mills was the first person who presented an existential formula and his pretty theorem is:

6.2. Mills’s theorem

A real number like "a" exists so that  generating prime numbers.

After Mills this theorem extended by Kuipers in below form.

6.3. Kuipers’s theorem

For every integer number a real number like "a" exists so that generating prime numbers, later the obligation of integrity for "c", became removed.

6.3.1. Generalization of Mills’s theorem

If  be a real number, then a real number like "a" exists that generating prime numbers . At last Niven proved below theorem:

6.4. Niven’s theorem

For every real number  a real number like "a" exists so that generate prime numbers.

 

Note that real number "a" in above theorems isn’t unique.

6.5. Formulas of generating prime numbers

Till now, we mentioned some attempts for finding a formula to define and also finding functions that their values exclusively be prime numbers for natural numbers. In this subject, we express some of results, obtained recently. As it clears soon, obtained results although they are charming and pretty, but couldn’t solve the problem. Origin of them is pretty Mills’s theorem (1947). But for training reasons, at first, we express some of simple results that for proving them, it isn’t necessary to be acquainting with primary properties of sequence and real numbers set. Some Primary Results:

6.5.1. Theorem

If:

      (1)

Then:

                          (2)

 

Proof. We know that. So series in formula (1) is concurrent:

 

 

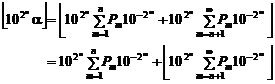
But:

 

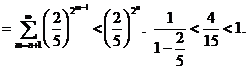
So:

And it is clear that

Therefore:

.

6.5.2. Remark

Formula (2) of above theorem hasn’t useful advantage.

Because, for calculating "" by this formula, it must calculate value of ""to  digits of decimal and this need to know the values of.

6.5.3. Attention

Another formula also exists that has this defect. For example, another interesting formula that was found for finding prime number by using the prime numbers less than it was propounded by Gandhi in Moscow Mathematicians congress in 1966.

6.5.4. Gandhi’s Theorem (1966)

 If "" is considered as n^th prime number and () as obvious function and  then  is calculated from the below inequality:

6.5.4.1. Note

For every real number "a", maximum one integer number "k" can be found so that:

Proof. For proving this theorem, we put:

So:   

That "", but for every "", the term appears in above sum when "d" is a common divisor of "Q" and "t". So, coefficient of "" in this sum is:

 

But we know:

  So   (according to )

And now:

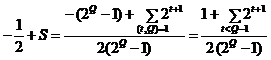
According to, for every integer number "m" that, a prime number smaller than  aliquots (). So, the greatest "t" which appears in is (). On other side:

 Therefore:

And with multiply this relation in

According to values of "P" and "S", it is obvious that this inequality is favorable inequality.

Introduction to Mills’s theorem

 Mills’s theorem is based on below theorem:

6.5.5. Ingam’s theorem (1937)

Constant number like "A" exists, so that for every natural number "n":

Proving Ingam’s theorem by properties of Riemann zeta function () is more than frame of this book. For proving next assertion, we accept it. In below, "A" means Ingam's constant.

6.5.6. Theorem

For every natural number "N" that is greater than _"", a prime number exists between and.

Proof. We suppose that and "" is the greatest prime number which is smaller than "". So, from theorem (6.5.5):

6.6. Generalized Mills’s theorem (1947)

 A real number which we call it _"" exists so that  is prime number for all natural values of "n".

Proof. We define "" by a sequence of prime numbers. We consider that "" be a prime number greater than "A". According to (6.5.6), a prime number exists between "" and "". We choose one of them and named it "". Generally, if prime number "" is defined, we consider that  is one of prime numbers between "" and "" and .

Now, we define and  sequences with below equalities:

 Sequence is instinctually ascending and  sequence is instinctually descending. Because:

    ,    .

Always . It is clear that two sequences are convergent and If, then always  so and according to (6.5.6):

Therefore for every natural "n":

6.6.1. Remark

Although proof of Mills’s pretty theorem indicates a method to define "" for making  sequence that "" is defined by it, we must obtain prime numbers which are great at pleasure and this needs to have a kind of formula for finding prime numbers. Mills’s theorem is developable. First extension of it was propounded by Kuipers who in 1950 proved that "3" hasn't fundamental role in Mills’s theorem.

6.6.2. Kuipers’s theorem (1950)

If "c" be an arbitrary integer number greater than "2"then a real number like "" exists so that  is prime for every natural number "n".

Proof. Proving the theorem is the same as prove of Mills’s theorem with a little change. If we suppose that  and, then So according to Ingam's theorem, a constant number like "B" exists so that for every natural number "n": . Now, we consider that "N" be a natural number and greater than "B" and "" be the greatest prime number smaller than. According to , . We will have:

.

Now, we can define the sequence of prime numbers like proof of Mills’s theorem by below relation:

And finish the proof in the same method.

6.6.3. Attention

 It is proved that for every:

 

6.6.4. Attention

If "" be r-th prime number, it is proved that if  then, a prime number like "q" exists so that:

6.7. Investigation into polynomials

Is there any polynomial so that answer the previous problem? Before expressing final result, we explain a little in this section.

I. If "p" be a prime number, value of, constant polynomial, is prime for all of values of "x", we delete this trivial case form this subject suppose that

     

Is a polynomial of first degree? If value of this polynomial be prime

number "p". For  we suppose that then:

Then for every value of "k" so that is a composite number, therefore it is impossible that the value of polynomial with integer coefficients from first degree be a prime number for all of integer values or positive and integer values of variable. Moreover, in this case, searching about terms value of  for integer values of "x" refers to arithmetic progression from integer numbers.

II. Some of second degree polynomials give long sequence of prime numbers. For example below three polynomials (Euler, 1772) that values of every one, are prime for integer values of "x" that is determined:

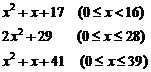
Values of polynomial are prime number for.

If we suppose that  it is clear simply:

So, is prime for and therefore is prime for and finally the values of below polynomial:

is prime for  namely , but it is not necessary to be distinct. Because, for every value of "x":

6.7.1. Remark

Some of mathematicians named "m" natural numbers as fortunate, when values of polynomial  are prime number for values of "x". From what is said above, it is clear that "41" is fortunate. Moreover, simply we can search that 2, 3,5,11 and 17 also are fortunate. In 1934, Hailberon and Linfot proved that just one of other fortunate number exists. And with calculation, it cleared that if such number exists, it will be very great. At last, in 1967 Setark proved that fortunate numbers are just such mentioned numbers.

It is clear that every non-constant polynomial with integer coefficients, assumes non- prime values. Proving below exact theorem is easy.

6.7.2. Theorem

If  be a non-constant polynomial with integer coefficients, set of integer numbers like "x" that for them,  is composite, is infinite.

Proof. We consider below polynomial has integer coefficients:

         (1)

And for every integer number like "", be prime. So, infinite integer number like "" exist that is a composite number.

 

And also:

That is an integer coefficients polynomial with respect to "y". Specially leading term is. So according to (1):

6.7.3. Remark

By interpolation the formula of LaGrange, always we can make a polynomial that for every number of determined arbitrary integer values of variable, its values be difference prime numbers. For example value of below polynomial:

 for  values of "x" respectively are equal to 3, 5, 7, 11, 13 and 17. But we don't know a polynomial of second degree or more than it that we can prove that its values are prime number for infinite numbers of "x" values. Specially yet we don’t know that polynomial has this properties or not. In this section there are some simple necessary conditions that we explain them below.

6.7.4. Remark

In order that values of non-constant polynomial with integer coefficients  be prime for infinite integer values of "x", necessary condition is that  be irreducible. It means that it isn’t decomposable to multiplication of two non-constant polynomials with integer coefficients.

6.7.5. Remark

Polynomial with respect to  variable doesn't exist that its values be prime number for all of integer values of variables. In this field, Yuri Matijasevich, Russian famous mathematician, in 1970, obtained a wonderful result that polynomial with respect to some variable exists so that all of its positive values are prime and in 1971, by using of Fibonacci's numbers designed for making a polynomial with respect to 24 variable and form 37 degree with mentioned properties and in completing his article, increased variables to 27 variables. But decrease degree to 31. We must name some of other investigator mathematicians that have interesting work in this field, like Martin Davis, Julia Robinson and Hilary Putnam. In 1976, James J. Jones (Canada), Daihachiro Sato (Canada), Hideo Wada (Japan) and Douglas wines (Canada) in an assay which printed in "American Mathematical Monthly (Vol. 83, number 6)", proved that set of prime numbers is adapted on set of polynomial's positive values with 25-th degree polynomial with respect to 26 variable a, b, c, ... z for all of non-negative integer values of variables.

This polynomial also takes negative values like (–76) (Quoted from mentioned assay).

6.8. A formula presenting for generating prime                             numbers by Wilson's theorem

 We suppose:

                                    

                                                (1)

So for every two natural numbers, "x" and "y",  is prime and moreover, when "x" and "y" run set of natural number,  gives every prime number and gives every odd prime number just one time.

Proof. We observe that values of  are just 2 and, because if , then . According to definition of "":

(2)          ,     (3)    .

In first case  is a prime number. In second case according to definition of "B",then. So according to converse of Wilson's theorem,  is a prime number. So, it is clear that for every two natural number "x" and "y", value of  is a prime number. Conversely, it clears that

f (1, 1) =2. If "p" be an odd prime numbers, with definition of:

So,  gives all of prime numbers. At last, for proving this assertion "Just one times" about odd prime number, It is enough to observe that according to what we said, if odd prime number "p", from , be obtainable, it must:  and therefore and so:

 

then  take value of "p" Just for value of "x" and  from "y".

 

At last we have to say that it is wonderful that a mathematician like Hardy[2] couldn't calculate such formulas that even he thought that such formulas don't exist. Because in a speech in 1928 in America, he said that for example "If some body wants me to write a formula for n^th prime number or calculate "" with respect to "", only I can say that he ask an erroneous question and probably such formula doesn't exist". I wish he content oneself with this sentence then he presented formulas and explanation to show that such formulas must not exist. Of course this speech was so important and later put it in collection of articles of MAA, that takes prize (The Chauvenet Papers). But it isn't credible that a formula which its existence needs just Wilson's theorem, be so far from mind of a mathematician like Hardy. If Hardy was alive now, he couldn't believe that he said such things sometimes.

In searching a rule that be commanding of prime numbers distribution, decisive stage traversed when mathematicians gave up useless trying for finding a simple mathematics formula that generating "all" of prime numbers and dispensed with definition real number of prime numbers that exists firstly on unit between "n" successive numbers and instead of them, attempts to obtain information about "average rate" of prime numbers distribution among "all" numbers.