CHAPTER 5
Decisive solution to the problem of recognizing prime numbers by
a formula concerning recognizing of numbers "
"
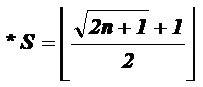
5.1. Determination of the formula for the characteristic function of numbers
At first we form a matrix of "0" and "1" for odd natural number and according to their divisibility on every odd number:
|
|
1 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
23 |
25 |
27 |
29 |
31 |
33 |
35 |
37 |
39 |
41 |
|
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
... |
|
3 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
... |
|
5 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
... |
|
7 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
... |
|
9 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
... |
|
11 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
... |
|
13 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
... |
|
15 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
... |
|
17 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
... |
|
19 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
... |
|
21 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.1.1. Explanation
If numbers in columns are divisible on the numbers in rows, their intersection, in the table has a value as "1" and if they aren’t divisible their intersection has a value as "0".
Ÿ First column has only "1" because all of numbers are multiplier of "1".
Ÿ Second column indicates multipliers of 3.
Ÿ Third column indicates multipliers of 5.
Ÿ And as it is seen, every column is multipliers of a number.
According to table rows, when in front of every column
number written just two number "1", in fact that column number is a
prime number because "every prime number is divided just on "1"
and itself". And knowing that "for identifying the primality of
specific number "N", it is enough that we divide "N"
on prime numbers which are not more than 
". For identifying column
number it is enough to attend row of that number. If in one row there are more
than two numbers "1", that number isn’t prime column number. For
example the row concerned to number "15", has four number
"1" , because it is divisible on 1,3,5 and 15 therefore
"15" is composite. But rows of (3, 5, 7, …, 17, 19, ...) have just
two numbers "1". So this numbers are Prime. For identifying the
numbers, it is enough that we find some functions that produce every one of
table column. In the other hand it produce all of "0" and
"1" in every column with same column arrange (from up to end).
General formula of these functions is:
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
3 |
1 |
1 |
0 |
0 |
0 |
0 |
|
5 |
1 |
0 |
1 |
0 |
0 |
0 |
|
7 |
1 |
0 |
0 |
1 |
0 |
0 |
|
9 |
1 |
1 |
0 |
0 |
1 |
0 |
|
11 |
1 |
0 |
0 |
0 |
0 |
1 |
|
13 |
1 |
0 |
0 |
0 |
0 |
0 |
|
15 |
1 |
1 |
1 |
0 |
0 |
0 |
|
17 |
1 |
0 |
0 |
0 |
0 |
0 |
|
19 |
1 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
According to the table and this point that for identifying
numbers "N", it is enough to divide it on prime numbers which
are not more than
, therefore, we divide "N"
on odd numbers which are not more than it, So for calculating odd number which
is not more than, sum of functions of the numbers
in column "x" is enough. Therefore, if "N" be prime,
we have just one number "1" in row of number "N":
("N" is prime number) 
If "N" is composite:
("N" is not prime number)
We know that "1" is neither prime nor composite
and also
,
therefore, if "N" be an odd number and greater than 
then:
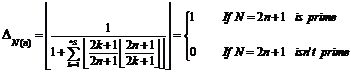(3)
That *S value is:
5.1.2. Attention
"
" is prime or composite and
these two cases will be determined by identification function 
and always
just two cases (3) namely "0" and "1" will be accrued.
Therefore, if we write a function by using it is a surjective function (in
the set of odd numbers that are greater than "3").
According to primary conditions, we form the below table:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
… |
50 |
… |
|
|
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
… |
101 |
… |
|
|
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
… |
1 |
… |
Now, we content oneself with present example two, for showing application of this function.
5.1.3. Example
At first we calculate *S for identifying the
number 
to
be prime or composite:
Then we form function
:
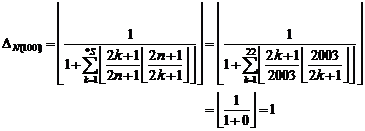
Since "
" so, number "2003"
is a prime number.
5.1.4. Example
For determining number"
" if we calculate like
example (5.1.3), it results:
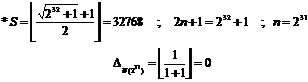
Since "
" so number "
" is a
composite number.
5.1.5. Result
According to above examples, It is observed that for
determining a number like "N", It is enough to calculate (
) by a simple
software program[1].
It is obvious that in this method, for determining number "N",
only answer of dividing "N" on all of odd numbers smaller than
are
used. Therefore, for determining number "N", we do the least
possible calculation by this method software program of this identification
function.
5.2. Formula for surjective characteristic function
If we want the identification function 
to accept 
, we can use
one of two below identification functions instead of it ():
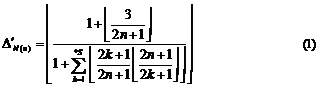
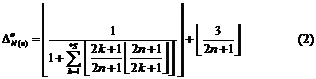
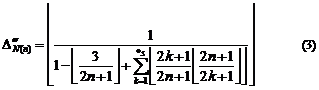
5.2.1. Attention
The number "*S" is same for
,
, 
and is
calculated by below relation:
Therefore, for every odd number greater than "1" (
):
