CHAPTER 20

Fundamental role of prime numbers and its properties in a complete investigation into Diophantine equations in the sense of existence or non-existent solution and presenting a general solution for the Diophantine equations:

Some of the generalizations:

            

Some of the general generalizations:

, 


20.1. Investigation into extension Fermat’s last theorem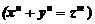

Before expressing details of Algebraic method of solution of Fermat’s last theorem that Andrew Wiles proved it, we express and solve the general equation:

       (1)

We can study equation (1) in two general forms:  and.

It is obvious that in case, in fact, we are face with the Fermat’s last theorem, because:

;

With thesis:

      (2)

In this section, we try to follow the story of Fermat’s last theorem (famous to Fermat’s great theorem) with reasoning method to acquaint interested persons to mathematics with manner of using Algebraic and geometric methods.

Also, we try to show applications of Wilson’s Euler’s and Fermat’s theorems in solving general equation (1) that is result of researches and continuous attempts of the writer of this book in "20" years and also propounding the last important algebraic results about Fermat’s last theorem that are obtained by the writer.

In this chapter, we follow the history of Fermat’s last theorem till 70s. Importance of this subject is in gathering details of algebraic methods that kummer used it for solving Fermat’s last theorem for the first time. For studying kummer’s works and mathematicians after him that completed his methods, there are a few references except special books. These methods used for many other problems besides attempts to prove Fermat’s last theorem. Therefore, acquaintance with them is useful for interested reader. This part is a sample reference for this purpose. Fermat’s last theorem was proved by Andrew Wiles by using the other mathematician's results after "350" years attempts in 1995. This proof is one of the most important mathematics successes in 20th century in which algebraic methods and geometric methods combined in a beautiful but very complicated manner.

            In this brief epilogue that has been written for mathematic interested persons who are not expert in Algebraic geometry, we try to acquaint the reader with some aspects of this proof. Our purpose is only explanation the relation between proof of Fermat’s last theorem and basic guesses in algebraic geometry and therefore, we do not prove the Wiles’s proof. We try only to give a general idea from this part of mathematics. It is clear that exact understanding the Wiles’s proof is not easy and needs to deep study in many years.

20.2. Primitive, Algebraic and geometric methods

 Fermat’s last theorem says that if,,  and "" be integer numbers and we suppose , then at least one of three numbers ,  and  will be zero. How can we prove such conjecture? Three manners for treating such problem are natural.

The first method is attempt in using the primitive methods of number theory. In such attempt, we do not use algebraic construction, theory of complex numbers and algebraic geometry and we use only the properties of divisibility of integer numbers. Usual proof of being surd of  is with this method .As we explained in this book; Fermat himself used these methods for the case of "". These primitive methods are not easy methods and we can gain many results about Fermat’s last theorem by using them. But if we adequate only to this methods we can prove only some special cases of Fermat’s theorem.

The second method is use of Algebraic methods. This section explains importance and application of Algebraic methods well and so we don’t explain it here again. Using these methods, Fermat’s last theorem was proved for all of integer numbers "n" that. Although Algebraic methods had important role in Wiles’s proof but they couldn’t prove Fermat’s last theorem alone.

The third method is using the Algebraic geometry. How can we use the geometry to solve a problem like Fermat’s last theorem?

Fermat’s last theorem is an assertion for integer numbers and at least, they haven’t usage in primitive mathematics for solving such problems.

We can show possibility of usage geometric reasoning by an example. Suppose that we want all of integer numbers which adapt in equation. With dividing both sides by:

If we consider  and. Then the problem is changed to find rational answers of below equation:

 

Every rational answer for this equation is an integer answer for the first equation and conversely every integer answer of the first equation (if) is a rational answer for the second equation. "" is equation of circle centered on origin and with radius of "1". Therefore, we must find the points on circle that their coordinates be rational numbers.

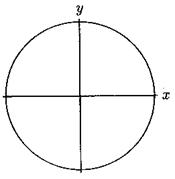
Figure 1.Circle

 

With the same method, finding integer answers for equations like  and other Fermat’s equations lead to find the points with rational coordinates on a curve in the plane:

 

            

 

Figure 2. Curves  and

 

It is interesting that according to Fermat’s last theorem, the first curve (circle) has many points with rational coordinates but on the next curves all of points with rational coordinates have a zero coordinate.

How do we find some points with rational coordinates on a curve? Solution is easy about a circle. Consider (x, y) as two points on the circle. Draw the straight line between point (-1,0) and point (x,y) (we suppose that ). We call (o, t) the place of junction of this line with axes. With calculation, it seems easily:

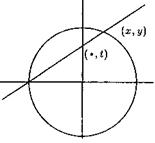
Figure 3.  Finding the points with rational coordinates on curve

 

It is resulted that is a point with rational coordinates and is on the circle with unit radius if and only if "t" is a rational number. So if  and "a" and "b" is integer numbers, then:

            (1)

So, for finding a point on a circle with rational coordinates, at first we choose two integer number "a" and "b" and then by using the formulas (1) we find coordinate of. Except the point all of points on circle with rational coordinate will be obtained. With adding some primitive reasoning, it is resulted that all of integer answers of equation "" are obtained with below equations:

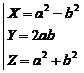               (2)

 

As we saw, using the geometric concepts for solving the Fermat’s equation when "", was very successful. Of course, we could also use primitive methods of algebraic methods.

It is very complicated for "". "Faltings" obtained the most successes in this field in 1986. He proved that many curves like curves "", have a limited number of rational point for. It results that for every given "n", the number of counter example for Format’s equation isn’t infinite.

20.3. An indirect proof of Fermat’s last theorem (elliptic curves)  

The method that was useful for proving Fermat’s last theorem wasn’t one of these direct methods. Of course, Wiles’s proof is based on algebraic geometry and he used the algebraic method a lot, but this proof, doesn’t prove Fermat’s last theorem directly. Direct usage of algebraic geometry means to find the points on curve  with rational coordinates. Some years before Wiles’s work, other mathematicians arranged new strategy for solving Fermat’s last theorem. Andrew Wiles concluded this new method. In the first look, this new method may look a little strange. This strategy is that we suppose that a counter example exists for Fermat’s last theorem. So, integer numbers,  and  exists so that

And,and. Number "C" is "" and with knowing  and  finding  isn’t difficult. But two integer numbers  and  must be interesting integer numbers. These two integer numbers are counter example of Fermat’s last theorem and mathematicians are looking for them around 350 years, so these two numbers must have other interesting properties.

Of course, this method is similar to shooting a bullet in darkness, but this method led to prove Fermat’s last theorem.

Mathematic element which is used in this strategy is elliptic curve. We express some properties of elliptic curves and then, we express its coherence with Fermat’s last theorem. Wiles’s proof not only proved Fermat’s last theorem but also proved important properties for elliptic curves. Elliptic curves have important role in algebraic geometry and so, information about them can be useful a lot.

20.3.1. Elliptic curves

Every non-singular cubic curve is called as an elliptic curve. Since we don’t need the most general (and the most precise) definitions, we restrict our self to the

 

curves with below equation:

      (1)

Other third degree equation can be changed to such equation without changing the curve properties.

It is a non-singular cubic curve if in every point has a well defined tangent and so hasn’t node or cusp. For such equations, we have other equivalent definitions for being non-singular like if:

And if below system of equations is without any answer:

Then, cubic curve (1) is non- singular (and then is an elliptic curve).With a little attention, it is resulted from the last definition that cubic curve (1) is non-singular if below equation have three different answers[1]:

         (2)

For example, the curve "" and curve "" are elliptic (figure 4). Origin of coordinates is a node (the double point) for curve "" and a cusp (the triplet point) for curve "". So, these two curves (figure 5) aren’t elliptic.

Briefly, definition of elliptic curve can be presented in algebraic geometry. Elliptic curve is a smooth projective curve of genus "1". In this book, we define elliptic curve as non-singular cubic curve that is illustrated in equation (1).

 

(a)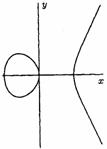               (b)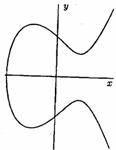          

Figure 4.  Elliptic curves  (a),  (b)

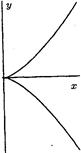 (a)               (b)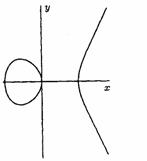

Figure 5. Non-elliptic curves (a), (b)

Note that we can’t guess only with definition of elliptic curve that this mathematic element has coherence with Fermat’s last theorem. Of course Fermat’s equation is an elliptic curve for "", namely  (as it was mentioned, this equation that is out of limit of this book, is a cubic curve equation from equation (1) kind). But Fermat’s equations with higher degree doesn’t form elliptic curve.

As it is said before, this proof uses elliptic curve unexpectedly.

20.3.2. Frey’s elliptic curve and Fermat’s last theorem

Using the primitive reasoning, we can prove that if a counter example exists then a counter example exists too with below conditions:

, and are three integer numbers that

I.   ,

II.  ,

III. Prime number exist that, and  are perfect n-th powers,

IV.  , and  haven’t a common factor,

V.    is divisible by "32",

VI.  .

VII.  .

Gerhard Frey, German mathematician suggested in 1985 that if, and  adapt in these conditions, then we can consider below elliptic curve:

         (2)

Frey thought that it must have very interesting properties. Note that because of given conditions, equation "" has three different roots and so equation (2) is a non-singular cubic curve and in fact it defines on elliptic curve. This elliptic curve is famous as "Frey’s elliptic curve".

20.3.3. Why elliptic curve?          

Equation (2) is a definition of a special elliptic curve based on a counter example on Fermat’s last theorem. But why we study this elliptic curve? The real reason is that elliptic curves have a lot of properties and because of this a lot of guesses exist about their manner.

Gerhard Frey wasn't looking for solving Fermat’s last theorem. He wanted to find an elliptic curve so that with help of it, he could evaluate some guesses about elliptic curves.

Here we obtain Taniyama- Shimura- Weil conjecture that proving a part of that by Wiles, led to solve the Fermat’s last theorem.

The important point about elliptic curves is that some points with rational coordinates on an elliptic curve form an Abel group! It means that we can define a kind of summation so that when we add two points with rational coordinates on an elliptic curve, the sum will be a point with rational coordinates on that same elliptic curve. More over for this summation we must have a neutral element (zero element) every point with rational coordinates must have inverse and our sum must have property of associativity. It isn’t easy and often it is impossible for            non- elliptic curves. Here we show this sum with some example.

            For real values, we can draw diagram of elliptic curve in two dimensional planes. In order to define the summation action on points with rational coordinates, in the first step, we must add a point to plane. We call this point as point in infinite and we consider by heart that this point is very for in  axis. Every straight line parallel with  axis cut this point. More over, we take in account this point as points with rational coordinates. Adding this point maybe strange for reader, but in fact, we must consider elliptic curve in a projective plane for defining the summation and this point is infinite and in fact, in one of points in infinite of projective plane. For continuing this subject, exact understanding from projective plane isn’t necessary and reader can consider the same normal Euclid plane with an additional point. We show this point in infinite with.

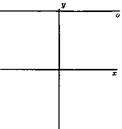
Figure 6. Point in infinite

In figure (7), we have drawn the elliptic curve of. The points  and, are points with rational coordinates on this curve. Now what is the point? You may think that we must add coordinates of "P" and "Q" together, but this action doesn’t give any point on curve. Definition of  is more complicated and is formed from two stages. At first, we draw a straight line passes from "P" and "Q". We can prove that this line crosses the elliptic curve in a third point with rational coordinates. In our example, this third point is. Now, we draw a line parallel to  axis from this third point (in fact, this line joins the third point to a point in infinite). Since diagram of elliptic curve is symmetric in relation to  axis, this line cuts elliptic curve in a forth point with rational coordinates. In our example, this forth point is. We call this point, so for curve we have:

Of course we can obtain a formula for this summation, but writing this complicated formula doesn’t help to understand this special summation.

 

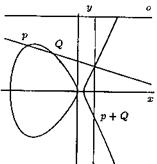
Figure 7. On curve  

We have

 

For better understanding, we need to another some examples. How is the summation of a point with itself? Only difference between this case and the general case is that we must draw tangent line in the given point, instead of the first straight line that passed from two points "P" and "Q". For example in figure (8), on elliptic curve, the point  is a point with rational coordinates. Tangent line in this point crosses the curve in point (4, 12), it means that for this elliptic curve, we have:

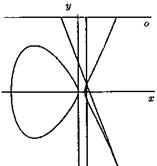
Figure 8. On curve

We have

 

How do we add a point with point "O"? The first straight line must be vertical and the second line is the same first line, so, it seems easily that result of summation of every point with point "O" is the first point itself. In other word, it is neutral in this summation and plays the role of "zero" .For example, in figure (9) for elliptic curve, we show:

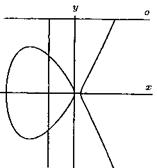
Figure 9. On the curve  

We have

 

In figure (10), again we show for elliptic curve that

In general case, if  is a point with rational coordinates on the same elliptic curve then  is also a point with rational coordinates and more over we have:

It means that for defined summation, every member has an inverse.

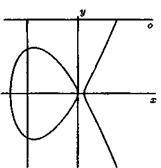
Figure 10. On curve

We have

 

Of course, this point that the points with rational coordinates and with this summand action form an Able group needs to be proved. We hope that the examples which we expressed convince the reader that this isn’t an unexpected assertion.

If  is an elliptic curve,  is indicator of Abel group of the points with rational coordinates. Now, we consider that reader has little information about able groups. Of course, our immediate purpose is discussion about some properties of. This discussion will convince the reader that information and open problems about points with rational coordinates on elliptic curves are very much. Details of this discussion have not so effects on understanding the rest of this book, so you can ignore them.

Every Able group like  is direct sum of the number of cyclic subgroups. Some of these cyclic subgroups are finite and the others are infinite.

We call direct sum of these finite cyclic subgroups as "torsion subgroups" of Able group. Torsion subgroup includes exactly the "elements of finite order". Every infinite cyclic group is "isomorphic" with group of integer numbers.

So, every Able group is direct sum of torsion subgroup and the number of subgroups that are isomorphic with. Every cyclic group has a "generator" but the number of generators of an arbitrary Abel group can be infinite. Mordell proved that the groups of points with rational coordinates on an elliptic curve can be produced by a limited number of members. Weil extended this theorem to "number fields".

20.3.4. Mordell–Weil theorem

If  is an elliptic curve then the number of generators of  is finite.

This theorem is important because we can consider some limits for structure of  without any information about. It is resulted from what is said about Able groups and by using the Mordell-Weil theorem that for every elliptic curve of:

That  and  are respectively "torsion subgroup" and "rank" of.

Knowledge about group  is not finished to Mordell-Weil theorem. Below deep theorem quotes that every group can not be the torsion subgroup of this group and it is restricted to only "15" distinguished groups.

20.3.5. Mazur’s theorem

If  is an elliptic curve and  is its "torsion subgroup", then  is one of these 15 below groups:

Here,  is indicator of cyclic group of order "m".

Mazur’s theorem is like a miracle. For example, suppose that you find a point with rational coordinates on an elliptic curve. We call this point "P". You can find "" by using the defined summation action. "", must be a point on an elliptic curve and with rational coordinates. With the same method,  and  and other points from "" kind that  is an integer value are points with rational coordinates on elliptic curve. Suppose that relation "" is established for point "P" .It means that rank of point "P" in group  is equal to "7". It is resulted from Mazur’s theorem that the only points with rational coordinates and finite rank on elliptic curve are. If another point with rational coordinates exists on this curve, then its rank is infinite. Searching about points with rational coordinates on elliptic curve is continued. Two open questions that their answers haven’t been found yet in this book are:

1) Can, the rank of "", be arbitrarily great?

2) Is there any practical algorithm for identification of being zero of?

20.3.6. Elliptic curves and finite fields

Consider  as a curve. We can that the points with rational coordinates on, formed an Abel group and we showed this group by. As the same method and with the same previous summation action, we show the points with real coordinates on  that formed an Abel group with . We obtain diagram of members of  when drawing  curve. Set of rational numbersand set of real numbers  are examples of fields. In a field, we have two actions of summation and multiplication and we can add, multiply, subtract or divide members of field (of course if it isn’t divisible by zero). Set of complex numbers  is another example of a field. Generally, if  is a field and  is an elliptic curve, then  forms an Able group. What is the purpose of? Members of  are pairs  so that "a" and "b" are members of  that adapt in descriptor equation of.

We explain it with an example. We consider "p" as a prime number and  as a finite field with "p" members. Then; and actions summation and multiplication are in "mod 7". So in F7:

We suppose elliptic curve  with below equation:

We can show that this elliptic curve has "5" points with rational coordinates (Note that we have put this condition that infinite point "O" is in every):

Every one of these points adapts in equation  and so if we consider them with, we obtain points in.

Attend that in "" we have  and so:

Of course, it seems directly that every one of these points adapts in equation. For example, if we put point  in equation:

That is correct with.

In the other hand  isn’t limited to these "5" points. We have also, because:

This example has "2" results:

1) If  then

2) The number of points  is limited forcedly. And so, finding is easy.

What is usage of ""? As we saw at the beginning of this section, finding  is used in a lot of cases in number theory but usage of isn’t very clear. In this section of Algebraic geometry, the key question is that can we obtain information about  with knowing   for different "p"?

For example, if for a prime number "p", we have, then it results that.

But what can we conclude in other cases? This question is important because finding is easy but knowing  has more value. If our considered equations were from degree "l" or "2" then Hasse-Minkowski theorem would give the positive answer to our question.

Here we don’t express this theorem because it isn’t adapted in cubic equations (and so in case of elliptic curves). In case of elliptic curves and may include a point, except  for all prime numbers "p" when.

But the story doesn’t finish here. There is a deep and miraculous relation between  and. Understanding this relation for primitive understanding from proving of the Fermat's last theorem is very important.

20.3.7. The number of members of

Consider below Elliptic curve:

We consider "p" as a prime number and we show the number of members of Able group "" with "". Since "" has only "p" members, "" is an integer number and finite. Like, for "", reader can see easily:

And then "". We remind that when we say "", it means that point adapts in equation "E". Of course all of arithmetic actions are done in field  and with:

We ask reader to find the members of, for at least two prime numbers of "p". It isn’t difficult but it convinces the reader that summation, multiplication and other actions change completely when "p" changes and consequently we can’t expect that any relation between "" and "" exists for two different prime numbers "p" and "". For example, compare members of "" which is given above, with members of "":

It is difficult to imagine any relation between "" and "" or between  and. Of course,  and it is twice of  but our target is a predictable relation

In below table, values of  are given for odd prime numbers up to "47":

P

3

5

7

11

13

17

19

23

29

31

37

41

43

47

Mp

5

5

10

11

10

20

20

25

30

25

35

50

50

40

 

The question is that is there any relation between these numbers? "Taniyama–Shimura–Weil" conjecture answer of this question beautifully. An interesting point about this answer is that its start point is in complex functions theory, namely in analysis. This relation between Algebra and analysis is very deep and unexpectedly. For understanding this conjecture reader must be patient and let us start from an apparently dissertated subject. More over, it isn’t strange that if reader is worried about general relation of this subject to Fermat’s last theorem. Interesting aspect of proof of Fermat’s last theorem is that its key part has no relation to Fermat’s last theorem.

Before every thing, we say that with reasoning it seems that  must have value about "". It is seen from the above table that approximately for any value of "p" this approximate value isn’t exact but may be it is acceptable that  and "" grow together to some extent.

For searching the relation between  and "", we consider some simple cubic curves. Consider the line.

The number of members of  is equal to "p" and every one of these "p" members can be substituted instead of  and so "p" point is obtained on the line. Always we take in account point  as a point on line. Then, at last "" points will exist on every line of. We can express the some reasoning for some kind of other curves. Like, again for, consider curve "". We must solve equation "" for every value of. This equation has answered generally that "" is a quadratic residue in. In number theory of primitive, it is proved that exactly half of numbers, "" are quadratic residue and if "" is a quadratic residue then equation "" has two answers.

The equation "" has one answer and usually we take in account  as an answer. It is results that if values of  are distributed among numbers,"" randomly and uniformly, then the number of points with coordinates in  on curve "" is equal to "". Therefore, for understanding sequence, we must attend to difference of  and "". We call this difference as "error term" and show it with:

Below theorem shows that this "error term" can’t be more than "".

20.3.8. Hasse-Weil theorem

"E" is an elliptic curve and "p" is a prime number. Usually  is the number of members of  and"" then:

Then for continuing the discussion, we come back to example  and as we promised before, we will use the analysis of complex functions.

Consider  and also below function:

            (3)

If we show the "complex upper half plane" by "H":

Definition includes multiplication of infinite terms. When we expansion this expression, a power series of "q" is obtained that in fact is "Fourier series expansion of function. Note that if we want  in this expansion, we must attend to the limited number of terms, because none of terms with "" has any role in coefficient of.

The question is that what coherence has this function with our subject? Find Fourier expansion of this function and if "p" is prime number, then put  equal to coefficient of  in this expansion. Finding  for small values of "p" is very easy (calculated by using "Maple software"), and these are in below table:

 

3

5

7

11

13

17

19

23

29

31

37

41

43

47

-1

1

-2

1

4

-2

0

-1

0

7

3

-8

-6

8

 

For seeing the importance of these numbers, we write also "" and "" in below table:

 

3

5

7

11

13

17

19

23

29

31

37

41

43

47

5

5

10

11

10

20

20

25

30

25

35

50

50

40

­

-1

1

-2

1

4

-2

0

-1

0

7

3

-8

-6

8

4

6

8

12

14

18

20

24

30

32

38

42

44

48

 

We see that "" that  is equal to the same error term. It is results that. In other word, in this special example, we could find a function that its Fourier expansion coefficients give error terms exactly. So by using them, we can find the number of members of  exactly. Of course, we may calculate  at first and then, we obtain Fourier expansion by using that. So only interesting point about function  is that  decompose easily. "Taniyama–Shimura-Weil" conjecture says that for every elliptic curve there is such function and more over, this function has good analytic properties. In fact,  isn’t a normal function but it is in "modular form".

Still we need more definitions for understanding "Taniyama-Shimura-Weil" conjecture and also a modular form and in another side, since this conjecture expresses an exact relation between elliptic curves and modular forms; we must express some other definition for elliptic curves. In fact, for this conjecture, some prime numbers are "good" prime numbers. So "Taniyama-Shimura-Weil" conjecture says approximately that if  is an elliptic curve then modular form of  exists so that coefficients of Fourier expansion  give error terms for in which "p" is a "good" prime.

20.3.9. Prime numbers of good reduction and conductor of an elliptic curve

Consider  as an elliptic curve and "p" as a prime number. If we reduce equation coefficients in mod "p", a new curve is obtained that maybe is singular or non-singular. If it is non-singular, it may have double point (node) or triplet point (cusp).

So, elliptic curve can be classified in three groups in relative to prime number "p":

1) If  be non-singular with mod "p", then "p" is a prime number of "good reduction" for.

2) If it has double point (node) with mod "p", then "p" is called as prime number of "multiplicative reduction" for.

3) If  has triplet point (cusp) with mod "p", then "p" is called as prime number of "additive reduction".

Prime numbers with multiplicative reduction or additive reduction are called as prime numbers of "bad reduction". More over, if  is an elliptic curve and all of prime numbers be good reduction or with multiplicative reduction, then  is called as "semistable".

Of course, the above definitions are not very exact. Here our purpose was that without entering to the details, we obtain a general over view of classification of prime numbers for elliptic curve. Another reason for inaccuracy of the above definition is that the configuration of descriptor equation of  may change by changing of linear variable despite  properties hasn't been changed. For example, consider "". This equation with  changes to equation "" that has triplet point and is singular, but we put in equation,  and, then equation  will be obtained that with  is "non-singular". A definition that changes with a change of linear variable can not be very useful. But the problem is raised from inaccuracy of above definition.

In fact, for every elliptic curve there is a "minimal polynomial" that has minimum possible value for those prime numbers of bad reduction.

Above classification of prime numbers must be used for minimal polynomial of every elliptic curve.

If  is an elliptic curve, then we define an important number for it. We show this number by  and call is as  "conductor". Here we don’t express the exact definition of  and we only say:

That set  is all of prime numbers. If "p" be prime number of good reduction, then  and if "p" be prime number of multiplicative reduction, then "". If "p" be prime number of additive reduction,  is an integer number greater than "1". The only deficit in this definition is that we have not defined accurately  for prime numbers of additive reduction.

Note that  is "semistable" if and only if  isn’t divisible by the second power of a prime number.

20.3.10. Modular forms

Modular forms have a distinguished position in modern mathematics and it seems that various phenomenon can be explained by using them. Here we express only general information. Some times we don’t express all of details since because of their difficulties, continuing its general subject will be impossible.  is the "upper half" of "complex numbers plane".  is a positive integer number. Consider below set of matrixes.

So members of are " matrixes" that their entries are integer numbers. Their determinant is "1" and their bottom left entry is divisible by.

 is a group. Action of this group is multiplication of Matrix. The important point is that this group "acts" on . It means that every member of group  gives a "permutation" of. In fact if  and  , then we can define  by using:

It is easy to see and for

We have. Attend that in left side of this equation, we combined permutations  and  while in right side of equation we multiplied two members of group  together.

Now consider "holomorphic" functions. If such function has some other properties except being "holomorphic" then we call it a modular form. Now we explain necessary properties of a modular form. Attend that as limited as this descriptor properties, then modular forms have more properties and it means more accuracy of "Taniyama-Shimura-Weil" conjecture.

The first condition is that integer numbers  and  exists so that for          

 we have:

Attend that for every arbitrary, matrix  is member of. If we calculate the above condition about this member we see that

It means that  must be a function with alternative period "1". It is resulted that such function has Fourier expansion and it can be written in below method:

This is Fourier expansion in zero. If we don’t have any negative power "q" in this expansion and in expansion  in other cusps of, then we call  as modular form of weight  at level. If in this  expansions, all "q" powers be positive (it means we don’t have power zero) then we call  as a "cusp form".

So, these modular forms are very special and therefore, this conjecture that coefficients of one of these modular forms give a lot of information about our elliptic curve is very interesting and unexpectedly.

The story doesn’t finish here. Set of modular forms of weight  at level  forms a vector space. On this vector space a sequence of interesting linear operators exists. Here we don’t express the definition of these operators and adequate only to their name. These operators are called as "Hecke operators".

If a modular form be "eigenfunction" of all Hecke operators it is called as "eigenform".

We repeat that for our subject, the details of these definitions aren’t very important. Only it is necessary to know that an eigenform is a special kind of a holomorphic function and so finding it during studying elliptic curve is like a miracle. Since eigenforms have a lot of properties, their relation with elliptic curves causes a lot of limits on these curves. One of these limits says that Frey elliptic curve can not exists and so we can not find a counter example for Fermat’s last theorem.

20.4. Taniyama-Shimura-Weil conjecture and Fermat’s last theorem

In 1995, a young Japanese mathematician (Yutaka Taniyama) propounded an interesting and bravely conjecture.

This guess became more accurate by "Goro Shimura" laters. The role of "Weil" is not clear and may be his role is limited according to this conjecture to other mathematicians. In today texts, this conjecture is known as "Taniyama-Shimura-Weil" conjecture. Now we can express this guess with more accuracy by using above definition.

20.4.1. "Taniyama-Shimura-Weil" conjecture

"" is an elliptic curve with integer coefficients and  is  conductor. For every prime number of good reduction "p", put

Then modular form  exists so that

1)  weight is "2", and

2)  is at level, and

3)  is a eigenform for Hecke operators, and

4) Fourier expansion  gives numbers.

Still, we don’t determine coherence of this important conjecture with Fermat’s last theorem. We said before that if Fermat’s last theorem is not correct, we can make an elliptic curve as Frey’s elliptic curve by its counter example.

Frey tried to prove, "Taniyama-Shimura-Weil" conjecture is false about Frey’s elliptic curve. It is resulted that if "Taniyama-Shimura-Weil" conjecture is correct then Frey’s elliptic curve can not exists. Therefore, we can not find a counter example for Fermat’s last theorem. "Jean Pierre Serre" showed that if another conjecture (that we don’t mention it here) be correct, then Frey’s assertion can be proved. American mathematician "Kenneth Ribet" could prove Serre’s conjecture in 1986.

20.5. Frey-Serre-Ribet theorem

Consider that  is a Frey’s elliptic curve. If we can find a modular form for  according to prediction to "Taniyama-Shimura-Weil" conjecture, then we can find this modular form so that its weight is "2" and at level "2" and more over this form be a cusp form. Such forms don’t exist!

20.5.1. Result

If "Taniyama-Shimura-Weil" conjecture be correct then Fermat’s last theorem is also correct.

Here we add this explanation that this solution isn’t the only solution of Fermat's last theorem. In late 80s, some other conjectures also existed besides "Taniyama-Shimura-Weil" conjecture that validity of every one of them led to proof of Fermat’s last theorem. Despite attempts of many experts of mathematician, these other conjectures have not been proved and still it isn’t impossible that one of these gives us a better method for proving Fermat’s last theorem.  Of course, at any rate, the first proof (and till now, the only proof) of Fermat’s last theorem is by "Taniyama-Shimura- Weil" conjecture.

Andrew Wiles proved "Taniyama-Shimura-Weil" conjecture for "half stable" elliptic curve and since every Frey’s elliptic curve is half stable Fermat’s last theorem was proved. Of course, Wiles’s primitive proof has an important mistake that it had been corrected by Wiles and Taylor later.

20.6. Wiles and Taylor-Wiles theorem

"Taniyam-Shimura-Weil" conjecture is correct for half stable elliptic curves.

20.6.1. Result

Frey’s curve is half stable and so Fermat’s last theorem is correct!

Here, we didn’t express Wiles's proof. This proof is a difficult and interesting that needs more than 200 pages.

Our purpose was that reader found relation between Wiles theorem and Fermat’s last theorem. In Wiles's proof, Galois's representations are used basically.

At last, we say that study in this mathematic course is continuing now that some years after Wiles’s proof in 1999, "Taniyama-Shimura-Weil" conjecture has been proved for all of elliptic curves (and not only for "half stable" elliptic curves).

For more information about proof of Fermat’s last theorem, refer to index of references.

20.7. Latest achievements and fundamental results concerning Fermat's last theorem and its extension (H.M) [2]

20.7.1. Fermat’s last theorem

Below equation hasn’t positive integer answer for :

        (1)

It is necessary to say that in this section, we suppose that equation (1) has positive integer answer.

Proof. Before proving the assertion, we express a basic and important conclusion about equation (1) that has a great role in proof Fermat’s assertion. This conclusion is extracted from proving "Mordell’s conjecture" by "Gred Faltings" that we mention it here just as conclusion.

20.7.2. Conclusion

The number of answers of equation (1) is finite only for.

20.7.2.1. Note. We mention about the last conclusion (20.7.2) that Mordell’s conjecture was propounded in 1922 and it is verified from geometric property of equation (1), namely it is proved for  that rational points on curve  are limited. Now, we express proof of conclusion (20.7.2) that is very important with Algebraic method.

 

Proof of conclusion ("H.M" method)

  At first we multiply equation (1) in:

           (2)

Equality (2) can be written in below form:

            (3)

Supposing  and, we write relation (3) in below form:

           (4)

We suppose common value of equation (4) as  that "p" is a rational number:

            (5)

Below equation is resulted from system (5):

           (6)

Expression of equation (6) is:

            (7)

It is obvious that since  is a rational number,  must be perfect square:

Equation (8) shows the necessary condition for solving equation (1). Namely in order to solving equation (1) for, there must be a general answer for.

We know the general answer of equation (1) for, therefore (according to (19.5)):

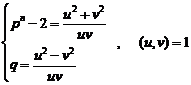         (9)

It is resulted from system (9):

 

 

Therefore:

           (10)

According to, it is obvious that, so equality (10) can be written in below form:

                    (11)

Since, so we must have:

                (12)

Substituting equalities (12) in equality (11):

              (13)

It is obvious that if  and, "p" value is rational and if and (even), so that be rational "p", we must have:

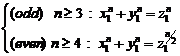          (14)

Here, two possible cases will exist:

I) If,  and are respectively smaller than,  and:

It is obvious that by continuing, unlimited Fermat’s reduction will occur and so equation (1) hasn’t answer except "zero" and therefore, Fermat’s last theorem is proved for "  ".

II) If,  and  are respectively greater than,  and:

It is obvious that with continuing, the next equations will be obtained and we will have below inequalities:

      (15)

With mathematical induction it is resulted from inequalities (15) that equation (1) can not have small answers for, and with supposition of existing answer for, it has very great answers and in fact when, the number of answers is limited and infinitely great. Here, conclusion (1) is proved in Algebra method[3].

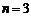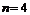20.7.2.1. Note. According to proof of Fermat's last theorem for "" and "" it is obvious that "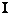" case happen, so for every "(odd)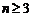" and "(even)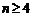" also "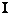" case happen, because procedure of proof is same for every"":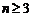

20.7.3. Conclusion (H.M)

In general case, equation (1) has property of reducibility to special case of every equation from below equations:

            (16)

For proving assertion (20.7.3), it is enough to write equation (1) in  form and multiply both sides of this equation in below expression and then rewrite it in form (16):

In fact, proof of assertion (20.7.3) is resulted from below equality:

        (17)

This very important theorem is extracted from proof of conclusion (20.7.3).

20.7.4. Theorem (H.M)

If one of the equations (16) hasn't any answer in form (17), then equation (1) will not have answer.

The explicit proof of this theorem is resulted from equality (17), because this equality shows reducibility of equation (1) to equations (16).

Here, another important result is that equation (1) isn’t independent to none of equations (16) about existence or none-existence the answer.

In other word, equation (1) depends on equations (16) about existence or non- existence answer.

Here, it is proved that equation (1) hasn’t independent answer and gains its answers from equations (16).

Also, in general case, below conclusion can be extracted from conclusion (20.7.3).

20.7.5. Conclusion (H.M)

In general case, equation (1) has reducibility property to special case of every below equations:

           (18)

In fact, equation (1) depends on general equations (18) about existence or non-existence answer and hasn’t any independence to infinite equations of (18) about existence or non-existence answer.

An important result that is obtained from theorem (20.7.4) is below theorem.

20.7.6. Theorem (H.M)

Necessary conditions for solving equation (1), is existing at least one answers in form (17) for every one of equations (16).

Important result from theorem (20.7.6) is that the hypothesis of existing answer for equation (1) necessitates existing answer for every one of equations (18). In the other hand, according to equation (8):

Primitive necessary conditions for solving equation (1) for every natural, is existing of a series of answers for equation (1) for. And according to reducibility property of equation (1) to equations (18), all of them have a series of special integer answers for.

20.8. Reducibility law (H.M)

The same power equation with index  is reducible to equations with index "".

For example, equation (16) is reducible to equations with index  for.

Explicit proof of this subject is resulted from below equality:

        (19)

      (20)

To gain the equality (20), it is enough to write equation (19) in form of:                            

 

and multiply the obtained equation in below expression:

Here, we can prove that if equation (16) has a special answer in forms like (17) or (20), in this special case it is reducible to equation (1). It means that for example, if equation (19) has an answer in below form:

         (21)

By using reducibility law, equation (19) is reducible to equation (1) that we multiply equation (1) in expression ­­:

 And according to equalities (21), we write recent equation in below form:

                              (22)

With the same method, if equation (1) reductions to below equation:

                             (23)

 Equation (23) must have an answer in below form:

          (24)

If equation (23) has an answer in (24) form, equation (23) reduction to equation(1):

According to below equalities:

Recent equation is written in below form:

           (25)

For reducing of equation (16) when, it is also enough to multiply equation (1) in "" that "".

Here, it is proved that hypothesis of existing answer for equation (1) led to an answer in the form of (17) for equations (16).

Also, it is proved that if every one of equations (16) have an answer in (17) form, then they are reducible to a special case of equation (1).

In the other hand, we know that in general case, equation (1) is reducible to every one of equations (16), therefore, hypothesis of existing answer for equation (1) for every  ruins the independence of equations (16) about existing or non-existing answer. Also it is proved that for, existing answer for equations (16) is necessary conditions for solving equation (1). So, Algebraic property of equation (1) namely its reducibility to every one of equations (16) or (18) is one of reasons that led to non-existing answer for it.

So, "Fermat’s last theorem" is proved with "Algebraic" and "geometric" properties of the similar exponents of equation (1) exactly.

20.9. Studying Diophantine equation of n-th order
(similar exponents) (H.M)

          (1)

Here before examination of equation (1), we propound an interesting Diaphontus problem. Euler arranged a series of assertions that are necessary for below hypothesis:

"For natural numbers  and  that adapt in condition, equation (1) hasn’t answer for natural numbers ".

It is obvious that when, Euler’s hypothesis changes to "Fermat’s last theorem". This special case of hypothesis shows that how much this problem is difficult.

For  and, we obtain the assertion of below unsolvable equation:

           (2)

In 1914, Werebrussov propounded proof of Euler's assertion about unsolvable equation (2). L.E. Dickson mentioned this Werebrussov's work in his book, but he didn’t point out that Werebrussov's proof is wrong. Only in 1935, w. Padhy attended to this mistake. E. Bell repeated this Werebrussov's mistake. M. Ward proved validity of Euler’s special assertion up to.

Euler's conjecture is wrong for  and  because:

           (3)

Also, for  and, Euler’s hypothesis is rejected because L.Lander in June, 27, 1966 found below numeral relation:

            (4)

Now, by using the "reducibility law" that having control over the similar exponents equations (1), we prove that many equations of (1) have answer for powers, "", and.

We saw that we can reduce equation  to every one of equations (1). Also, we can reduce below general equation to many equations (1):

             (5)

Here, we adequate to some examples.

20.9.1. Example

With hypothesis of existing answer for equation, an answer is obtained for equation (1). For solving the equation (1), at first we consider that an answer exists in  form:

Now, we write the above numeral relation in  form (or) and we multiply both sides of the above numeral relation in below numeral expression:

(

(or if we write in  form, we multiply numeral expression ( and after necessary summarizing , we have below numeral equalities:

(In first case)    

(In second case)

By comparison equation (1) with every one of last equalities, it is obvious that two series of answer are obtained for it:

(First answer)   

(Second answer)

20.9.2. Example

By using an assumptive answer of equation, an answer is obtained for below equation:

         (2)

For solving this equation, it is enough to put two answers of equation that made from an assumptive answer of equation  equal to each other (according to example (20.9.1)):

      (3)

After comparison equation (2) with numeral relation (3), an answer is obtained in below form:

20.9.3. Example

Equation  is solvable by using the assumptive answer of equation:

For solving above equation, at first we consider that an assumptive answer of equation  exists in  form:

Now, we write above numeral relation in  form (or or) and then multiply both sides of this equality in below expression:

After necessary summarizing, we have below numeral equality:

By comparison our equation with recent numeral relation, we obtain an answer in below form as the same method, two other answers are obtained):

20.9.4. Remark

By using the reducibility method, we can solve below equation:

with an assumptive answer of equation.

20.9.5. Example

Below equation has answered for,  and:

             (1)

It is enough to solve the below equation for,  and :

           (2)

At first, we write equation (2) in below form:

        (3)

We multiply both sides of equality (3) in conjugate of the second side:

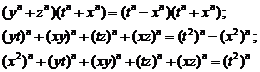            (4)

it is obvious that with reduce equation (2) to a special case of equation (1) for every natural , with hypothesis of existing an answer for equation (2), also, answer exist for equation (1):

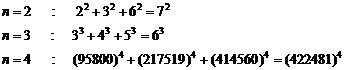
According to these numeral identities, three answers are obtained for equation (1):

Of course the smallest answer of equation (1) is in below form:

Also, a numeral answer for equation (1) for  of answer series (I) is in below form:

After dividing this equality by , we have the smallest answer of equation (1) for:

                      (5)

And a numeral answer of equation (1) for  of answer series (1) is also in below form:

20.9.6. Attention

In fact, equality (5) is equal to:

    or   

20.9.7. Example

Below equation has answer for ,  ,  and :

                      (6)

For determining an answer of equation (6), it is enough to solve the equation (2) for,  and :

Since this equation is reducible to special case of equation (6):

                       

        (7)

According to mentioned numeral identities, there are answers for equation (6) so that one of these answers is in below form:

 

Therefore, an answer of equation (6) for,  and  will be obtained by substituting the below values in (7):

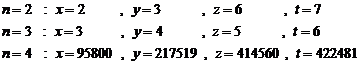
For determining an answer for equation (6), we can use below equation’s answer:        (8)

Because equation (8) can be reduced to a special case of equation (6):

 ;

          (9)

Therefore, an answer for equation (6) can be resulted from below numeral identities:

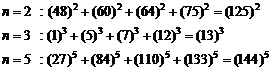
So, an answer of equation (6) for,  and  can be obtained with substituting below values in (9):

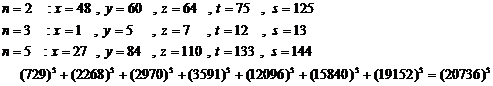
20.9.8. Extension (H.M)

Here, according to present numeral identities in cases,, and , we can present an answer for below equations:

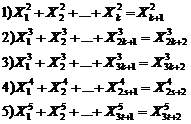
An answer series of these equations will be obtained with "H.M" reduction method in below form:

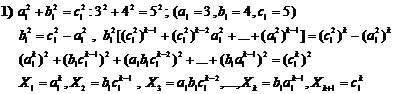
a special answer of equation (1) is:

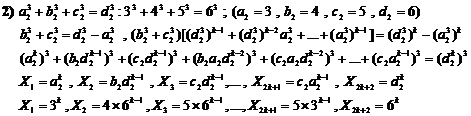
 Two another answers series of these equations (2) will be obtained with "H.M" reduction method  and we can obtain the equations answers of (3), (4) and (5).

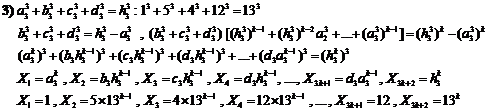
We will be obtained three another answers series with changing of,, and .

 

4)

    

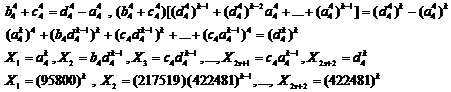
We will be obtained two another answers series with changing of, and.

5)

   

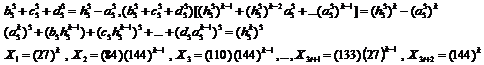
We will be obtained three another answers series with changing of,,  and.

20.9.9. Result. Here, we show that solve every same powers equation solving another same powers equations. If exist an answer for below equation:

           (1)

The below equations has answer also:

         (2)

If considered an answer of equation (1) in below form, we will be obtained the answers with changing,, ... and:

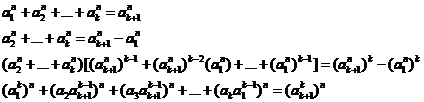
So:

20.9.10. Example

If, determine a general answer series of below equation:

      (6)

Solution. It is enough to compare equation (6) with below identity:

    (7)

By comparison equation (6) with identity (7):

20.9.11. Example

Determine an answer series of below equation:

        (8)

Solution. At first, we determine the smallest common multiple of equation powers:

According to this point that the smallest common multiple of equation power is number 1384, we can write below identity:

              (9)

By comparison equation (8) with identity (9), an answer series with two arbitrary parameters will obtain for equation (8):

20.9.12. Example

Determine an answer series of below equation:

     (10)

Solution. At first, we determine the smallest common multiple of equation

 

powers:

According to the smallest common multiple of equation powers (555385), we can write below identity:

     (11)

By comparison equation (10) with identity (11), an answer series of equation (10) is obtained with "1384" arbitrary parameters:

20.10. Solving Diophantine equations having non-similar exponents (multi-equalities) (H.M)

In below general equation, if  are different numbers, we can present an answer series for it:

     (1)

For determining a general answer series of equation (1), it is enough to compare it with below identity:

 

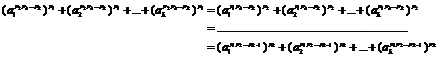    (2)

 

By comparison the equation (1) with identity (2), an answer series with "k" arbitrary parameter is obtained for equation (1):

 

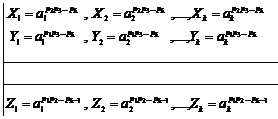
20.10.1. Example

Determine a general answer series of below equation:

            (3)

Solution. For determination a general answer series of equation (3), it is enough to compare it with below identity:

   (4)

By comparing equation (3) with identity (4):

20.10.2. Example.

If, determine a general answer series of below equation:

          (5)

Solution. It is enough to compare equation (5) with below identity:

20.10.3. Problems

Determine a general answer series of below equations.

 

 

 

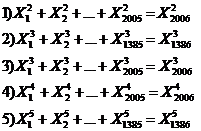
20.11. Finding an answer for extension of Fermat’s last theorem using                the theorems related to prime numbers (H.M)

      (1)

Before examining the equations like (1), it is necessary that we remind basically theorems related to prime numbers like Fermat’s "small" theorem, Euler’s theorem (an extension of Fermat’s "small" theorem ) and Wilson’s theorem .In order to this purpose, at first , we express the title of theorems.

20.11.1. Fermat’s "small" theorem

If "p" be a prime number and, then:

20.11.2. Euler’s theorem

If  then:

20.11.3. Wilson’s theorem

If "p" be prime number:

Here, it is enough that we present a simple proof for Euler’s theorem, because two other theorems are special cases of Euler’s theorem.

Proof of Euler’s theorem (2)

If  and we suppose that  and "n" is simple pack of residue with module "m" and. It is obvious that numbers  are also simple packs of residues with module "m", because:

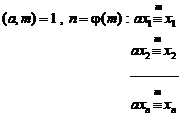
By multiplication of congruencies:

Since, after necessary summarizing:

20.11.4. Explanation

 (Euler’s Function): the number of numbers smaller than "m" that are coprime with "m".

Proof of Fermat’s "small" theorem (1)

It is obvious that if "m" be a prime number like "p", Euler’s theorem changes to special case, namely Fermat’s "small" theorem:

 

Proof of Wilson’s theorem (3)

In Fermat’s "small" theorem, we can suppose  or and "p" is a prime number greater than "2", and.

So, special case of Fermat’s "small" theorem is:

                 (Leibniz's theorem)

                              (Wilson's theorem)

­By testing, we find that answer of  and  are external and this is also established for.

20.12. Determining a general answer for equation (H.M)

         (1)

For determining an answer series of equation, at first, we calculate an answer series for below equation:

          (2)

For determining an answer series for equation (2), it is enough to compare it

 

with below "H.M" identity:

         (3)

By comparison equation (2) and identity (3):

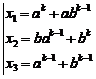
Here, if, equation (2) changes to below equation:

         (4)

(is Euler’s function ) : The number of natural number smaller than "n" that are coprime with "n" for example and , because 1,5,7, and 11 are coprime with 12.

According to Euler’s theorem, if, then expression  is divisible by "n", in the other hand, we can write:

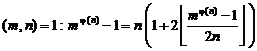          (5)

( : Integer part of number)

Using relation[4] (5), we write equation (4) in below form:

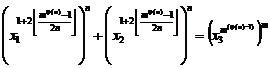             (6)

By comparing equation (1) with identity (6), an answer series of equation (1) is obtained:

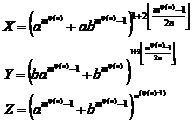                (7)

20.12.1. Explanation

In equalities (7), if "n" is a prime number like "p"

And if "m" be a compound number in form,

(p, q, t,… are prime factors) we can write:

For example:

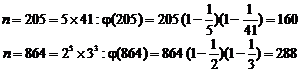
20.13. Determining a general answer for equation (H.M)

            (2)

Equation (2) is a special case of equation  therefore, for determining its answer it is enough to choose or  in answer of recent equation:

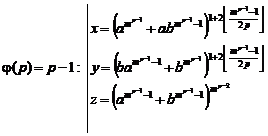               (8)

Answer (8) is a special case of answer (7) for. Of course, answer of equation (2) is calculable directly. Using Fermat’s "small" theorem and the same method of solution of equation (1), we can obtain answer (8) for equation (2).

20.14. Determining a general answer for equation (H.M)                     (The Fermat-Catalan 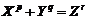conjecture                                                                 and the Beal conjecture)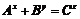

1.                      

(Prime number)  ,                  (3)

For determining an answer series of equation (3), at first we obtain an answer series of below equation:

                     (4)

For determining an answer series for equation (4), it is enough to compare it with below "H.M" identity:

                (5)

By comparing equation (4) with identity (5):

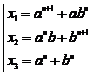              (6)

Here, if, equation (4) reduces to below equation:

               (7)

According to Wilson’s theorem, if "p" be a prime number, expression  is divisible by "p" and in the other hand, we can write:

              (8)

(: Integer part of number)

Here, by using the relation (8) and according to condition, equation (7) can be written in below form:

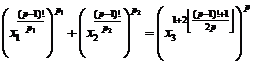        (9)

By comparing equation (3) with identity (9), an answer series of equation (3) will be obtained:

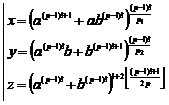
20.14.1. Attention

In above identities and equations, if we convert "p" to, we obtain the above identities and answers that always are established for. (: prime number formula).

20.14.2. The Fermat-Catalan conjecture

There are only finitely many triples of coprime integer powers "" for which

   with   

For example:

 ,      ,  

20.14.3. The Beal conjecture

Let " and" be positive integers with. If then  and have a common factor..

Or, slightly restated:

The equation "" has no solution in positive integers " and" with "and "at least "3" and " and" coprime[5].

20.14.4. The "" conjecture

We suppose "" is the product of the prime divisors of "" with each divisor counted only once. The "" conjecture can be formulated as follows:

For each  , there is a constant such that if "" and "" relatively prime (or coprime) and

Then:

Max.

20.14.5. Note.

We can show that if the "" conjecture holds then there are no solutions to the prize problem when the exponents are large enough[6].

20.15. Determining a general series of answer for Diophantine equations with arbitrary degree by using Wilson's, Fermat's and Euler's theorems and the role of prime numbers formula in arising of Algebraic identities (H.M)

Equation 1:

Prime numbers     

Equation 2:

 Prime numbers   ,     

Equation 3:

                                 ,  

20.15.1. Equation

Prime number, Natural numbers

  , 

For example:  

            ()

According to solution of equation (), (20.14) we investigate the extension of this equation and start this section with below title.

·        Solution of "p-th" degree equation in below general form and determining an answer series for it:

             (1)

In equation (1), "p" is a prime number and  are arbitrary rational numbers and.

Solution. For solving equation (1), at first we solve below equation and obtain an answer series for it:

             (2)

For solving equation (2), it is enough to compare it with below "H.M" identity:

       (3)

Comparing equation (2) and identity (3):

(4)                   

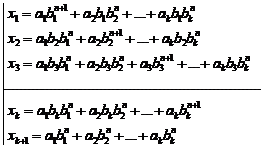
Here, if, then equation (2) reduces to below equation:

              (5)

According to Wilson’s theorem, if "p" be prime, then expression is divisible by "p" and in the other hand it is proved that for every decomposable expression[7]:

             (6)

(In relation (5), "p" is a prime number and  is symbol of integer part of number).

Now, by using the relation (5) and according to condition: , equation (4) can be written in below form :

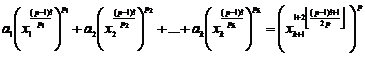    (7)

Comparing equation (1) with identity (6), an answer series of equation (1) will be obtained immediately (in identity (6) we can substitute  (prime numbers formula) instead of "p", then variable domain will extend to set of natural numbers (IN), because for every value is prime ):

(8)         

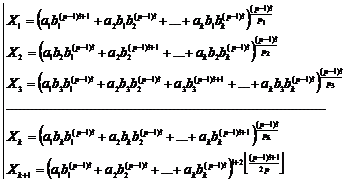
20.15.1.1. Example

Examine below equation and find a general answer series for it.

            (9)

Solution. It is enough to substitute below values in relations (8):

Therefore, a general answer series of equation will be obtained:

(A general answer series of equation (9))

(10)                

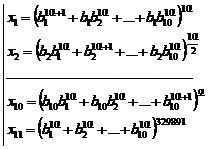
So, with this answer, equation examination is finished.

20.15.2. Equation

Prime number, Natural numbers and

For example.  If, then:

        (II)

Considering the solution of equation (II) (20.13), we examine the extension of this equation.

Ÿ Solution of n-th degree Diophantine equation in below general form and determining an answer series for it:

            (1)

In equation (1) "p" is a prime number and  are arbitrary rational numbers and "p" and "m" are coprime namely.

Solution. For solving equation (1), at first, we solve below equation and obtain an answer series for it:

            (2)

For determining an answer series for equation (2), it is enough to compare it with below identity "H.M":

    (3)

So:

(4)         

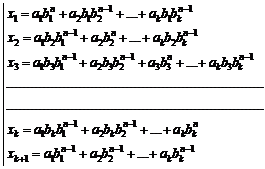
Here, if, equation (2) changes to below equation:

     (5)

According to Fermat’s (small) theorem, if "p" is prime number expression "" is divisible by "p" ("m" and "p" are coprime), in the other hand we can write:

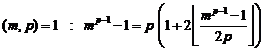         (6)

(In relation (6), "p" is prime number and is integer part of number)

Now, by using the relation (6), equation (5) can be written in below form:

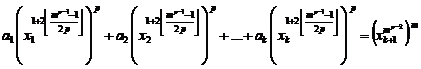        (7)

By comparing equation (1) with identity (7), an answer series of equation (1) is obtained immediately:

(8)     

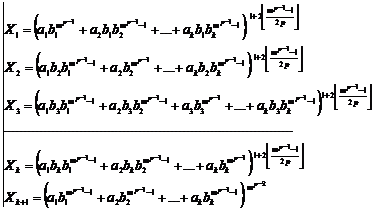
20.15.2.1. Example

Find an answer series of below equation if.

             (9)

Solution method. It is enough to put in relations (8):

So, an answer series of equation (9) is obtained immediately:

(10)      

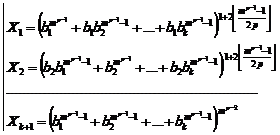
20.15.2.2. Result

In special case, if  then:

              (11)

Equation (11), always has answer for every prime number "p" if. Therefore equation (11) is indicator of this principle that sum of the same powers of two numbers can be written as a power of number if powers be coprime.

In the other hand, if "m" is not a multiple of "p" namely, then equation (11) always has answer, also if, equation (9) always has answer.

20.15.3. Equation

, Natural numbers

For example. If, then:

                                                            ()

Considering the solution of equation () (20.12), examine the extension of this equation.

Ÿ Solution of Diophantine equation in below general form and determining an answer series for it:

            (1)

In equation (1), are arbitrary rational numbers "m" and  are coprime namely.

Solution. For solving equation (1) and determining an answer series for it, at first, we obtain an answer series of below equation:

             (2)

For determining and answer series for equation (2), it is enough to compare it with below "H.M" identity:

      (3)

By comparing the equation (2) with identity (3):

(4)    

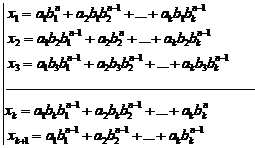
Here, if  equation (2) reduces to below equation:

               (5)

In equation (5), is Euler's function and  is the number of natural numbers and smaller than "m" that are coprime with it:

Set of number that are coprime with 18 = {17, 13, 11, 7, 5, 1}; .

20.15.3.1. Point

Always attend that number "1" is coprime with all numbers grater than "1".

According to Euler's theorem, if, then is divisible by "m".

In the other hand, we can write:

         (6)

(In relation (6), "p" is prime number and is symbol of number integer part).

 

Now, by using the relation (6), equation (5) can be written in below form:

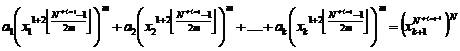  (7)

By combining the equation (1) with identity (7), an answer series of equation (1) is obtained immediately:

(8)      

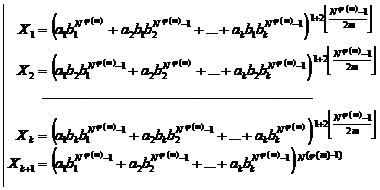
20.15.3.2. Attention

If "m" is a prime number like "p", then and if "m" is composite and in form (that "p", "q" and "t"…, are prime factors), then always we can write:

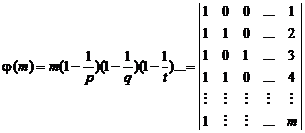           (9)

For example. We calculate  for "m=1024", "m=1025" and "m=1026", from relation (9):

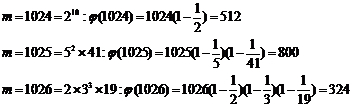
20.15.3.3. Example

If  ("p" is prime number) then equation (1) reduces below form:

Solution. It is enough in relation (8), we must put  in stead of.

Abstract of SOLUTION (1)

"H.M" Method

20.15. . Result (1)."H.M." theorem

 

If:  

  ,    Prime number ( p)[8] 

 

Then below equation has an answer:

               

Proof:

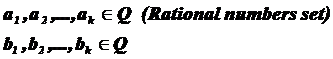
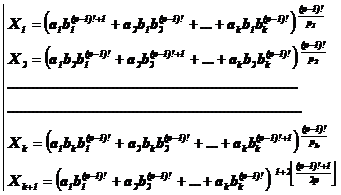
 Abstract of Solution (2)

"H.M" Method

20.15.. Result (2) . "H.M" theorem

 

If:

, ,  Prime number (p)[9]

Then below equation has answer:

 

 

Proof:

 

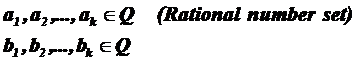
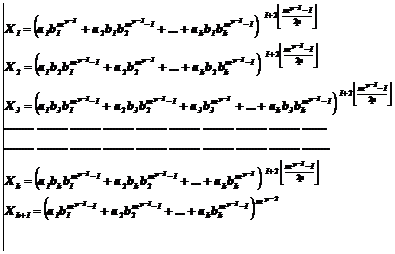
Abstract of Solution (3)

"H.M" Method

20.15.. Result(3). "H.M" theorem

 

If then below equation has answer:

       

Proof:

 

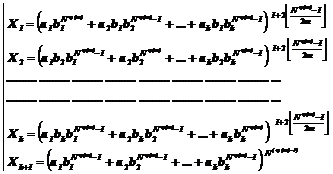
(Euler’s   Function)

 

1.  (Prime number):

2. (Prime numbers): 


---

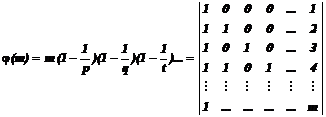
[1]. For more information look at the appendixes I (21.4) in the end of this book.

[2]. All of these conclusions are results of "20" years researches of writer about "Fermat’s last theorem".  

[3]. In fact, case (II) is caused from geometry-Algebraic property of equation (1), namely being limit of rational points on curve.

[4]. For more information look at the appendixes I (21.7).

[5] . The prize. Andrew Beal is very generously offering a prize of "$ 5,000" for the solution of this problem. The value of the prize will increase by "$ 5,000" per year up to "$50,000" until it is solved. 

[6] .Adapted from: A generalization of Fermat's last theorem, "the Beal conjecture and prize problem"(R. Daniel Mauldin) "mauldin@unt.edu".

[7]. Author proved this subject in a frequently applied theorem in appendixes I (21.5) in the end of this book.

[8]."p" belongs to set of prime numbers and we can substitute  namely prime numbers formula instead of it:

   (Domain of new variable)

[9].We can substitute  instead of (: Domain of new variable).