CHAPTER 12
On the history of attempts for solving Riemann zeta equation
"
" and the low of rarity of
prime numbers
12.1. Riemann’s Zeta function and its celebrated equation "
"
In this section, we want to express simply and preliminary, some of important results which Riemann obtained about prime numbers a century ago.
Riemann’s research was based on the famous function
"
" that is determined by
the below relation:
(1)
If the real part of "s" is greater than unit, the series in the other side will be convergent. It can be written simply:
(2)
In second side of this relation, all prime numbers has been shown, because whole integer numbers exist in relation (1). In fact:
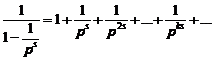(3)
And if we multiply all equalities like (3) with together:
(4)
In which
, 
, …, 
powers
can have all possible powers from zero to infinite so that every combination of,
, …,, will be
repeated only one time. It results that relation (4) is equivalent with
relation (1), because every integer number can be factorization to prime
factors multiplication, just in one feature. Riemann proved some properties of 
and
he guessed that some of its other theorems are probable. After Riemann death a
lot of mathematicians spent time to investigate. Among these
scientists, we must mention "Hadamard" and "poison" that
could prove Riemann’s basic theorem and its results "Rarefaction of prime
numbers". This law is based on that the number of prime numbers which are
smaller that "x", is asymptotically equal to:
(5)
So, approximately:
But it is resulted from relation (5):
(6)
And because "
" is so
little in comparison with
, we can write approximately,
instead of relation (5):
(7)
A lot of works have been done (and it is not possible for us to mention them) for obtained the relations (4) and (6), and it is impossible to find an exact simple relation by which the number of prime numbers can be obtained. We content oneself with this short information from advanced analysis and it is more than the subject of this book. In this section, we adequate to find a primary method for proving asymptotic relations (4) and (6) by which, the reader can gain a minimal information in this field. In any case, it is necessary to know preliminary properties of logarithm and exponential functions, because the relation which must be proved, contains logarithm also we use fundamentals of combination theory (Pascal’s triangle).
12.2. An introductory method for finding a fundamental
formula for "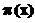
"
With symbol 
we show
the number of "
" combinations of "m"
to "m". Knowing that
(1)
And it is the same number which is in the 
th
rank of ()th row of Pascal’s
triangle:
|
1 |
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
1 |
2 |
1 |
|
|
|
|
|
|
1 |
3 |
3 |
1 |
|
|
|
(2) |
|
1 |
4 |
6 |
4 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
For example, for
we have 
and
also generally is the same coefficient of 
in
the expansion of
. If we suppose that "x"
and "y" are equal to unit, then:
(3)
Inequality (3) can be completed with below inequality:
(4)
In fact, according to relation (1):
(5)
Now, if we delete the equal factors:
(6)
Immediately, it results that the second side is smaller than unit, because every odd number is smaller than every even number in the same rank. But this relation can also been written as below:
(7)
And it is clear that the coefficient 
in
second side of relation (7) is greater than unit, because every odd number is
greater than its previous even number. Then relations (6) and (7) prove
inequalities (3) and (4). These inequalities can be shown by below equivalent
relations:
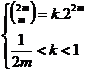(8)
It is not difficult to prove that asymptotically:
(9)
That "a" is a constant value, but
relations (8) is enough for our purpose. Now we change the integer number 
to
first make (1) and its factorization. If "p" is an
undetermined prime number smaller than 2m, it is necessary to clarify
the power of "p" in which exists in the numerator and
denominator of. In a preliminary calculation,
we considered that some numbers smaller than 2m, can be divisible by the
power greater than "p", in relative to 2m.
In the other hand, when integer factors of numerator and
denominator are divisible by "
", we
encounter it as a number which is divisible only by "p".
Factors of "2m" which are divisible by "p" are:
(10)
At last, we gain the greatest possible number "hp" that is smaller or equal to "2m", therefore:
(11)
It is better to distinguish the conditions in which "h" is an even number from the one in which "h" is odd.
First we suppose "h" is an even number
then:
(12)
That result the below inequalities:
(13)
So, the prime factor "p" is present
"2q" times in 
and "q"
times in "
" and therefore it doesn’t
exist in "" i.e. the quotient of on
square of .
Now, we suppose that "h" is equal to the
odd number "
":
(14)
And it results:
(15)
With this difference that now the factor "p"
is present in numerator by 
times and in denominator
only by "
" times and therefore one
time in the quotient of .
So is equal to multiplication
of prime numbers of "p" that adapt in inequality (12), except
the numbers which adapt in inequality (14) and contain "q" as
the representative of an arbitrary integer number.
Therefore:
(16)
Symbol 
extends for prime numbers
of "p" which adapt in below relations:
(17)
......................
Inequalities (17) must be continued until the prime
number of "p" adapt in them. Note that the second side of this
inequalities can not be prime numbers, because they are divisible by
"2" and therefore the symbol 
can be
changed to symbol <.
If we consider "L" the sum of limited intervals of two modalities in inequalities (17):
(18)
The series in parenthesis should stop when inequalities (17) don’t determine any prime number, but if "m" is a very great number, we can ignore little error and continue it to infinite.
So it is equal with "
" and it
is like that we put "1" instead of "x" in below
relation:
(19)
and the value of "" is
smaller than "0.7".
In other side, according to relation (8):
(20)
It is possible to write relation (16) in below form:
(21)
"L" is the total length of 
intervals
which contain the prime numbers "p" (in first side of equality) and 
is also
very little in comparison to "L".
Now we prove that this formula is established also when powers of prime numbers are available (we didn’t consider it in primary calculation).
The only difference is changing in value of "",
but again it remains very little in comparison to "m" and
"L".
In fact, the number of numbers smaller than ""
and divisible by square of an integer number like "
",
is maximum:
And if "" is
greater than "" ("p" is
greater than
), it is equal to zero. It is
clear that the number of factors of "p" is also smaller than ,
because "L" is the representative of length of "m"
in relation (21) and additional terms can be accumulated in "".
Never the less we establish our calculations based on correctness of relation (21) and then we compare the rustles with statistical calculation.
We consider "
" and
"
" as two prime numbers near
to each other, but there are some other prime numbers between ""
and "". We write the below
relations:
(22)
(23)
In which
and 
are
expressed by prime numbers smaller than "" and
"". If we diminish equations
(22) and (23) member by member, then:
(24)
In which 
is related to prime numbers
between "" and "",
logarithms average value of these prime numbers is equal with ,
in which, "x" is an unknown number between ""
and "".
If we represent the number of prime numbers between
"" and ""
as 
, then relation (24) can be
written as:
(25)
And it results the below relation:
(26)
According to the relation we can obtain the number of
prime numbers between "" and "".
If "" and ""
become near to each other, we can consider "x" as an arbitrary
number between "" and "".
And if difference between "" and ""
is great, we can consider "x" as a geometric average or
arithmetic average of "" and "".1 We will see that relation (26) adapts
with statistics calculations. We want to calculate the summation:
(27)
That contains all prime numbers up to "p"
(and the number "p" itself). We consider "
" and "
" as a little interval
between "2" and "p" in which there are 
prime
numbers so that some values of 
which are
equal to values of "" and "" adapt with them. Therefore
sum of these values is:
(28)
And finally, sum of S (p) is determined by the below relation:
(29)
That is sum of series of intervals between "" and "" that include all intervals
between "2" and "p". According to definition of
determinate integral:
(30)
If this integral be concurrent when "p"
approaches to infinite, 
will also exists.
If in a special situation, we consider
,
the below important relation will exist[1].
(31)
We know that if we consider all of integer numbers, approximately:
(32)
Great difference between relations (31) and (32) is one of mathematics operation that shows "rarefaction" of prime numbers.
Using the relation (31), results the below multiplication:
(33)
That includes the numbers between "2" and "p". In fact, when "p" becomes great the approximation gives:
(34)
So that asymptotic value of 
is:
(35)
Terms like
, 
and etc which have been deleted
in (34), form a concurrent series that when "p" tends to
infinite, will result a determinate factor.
Therefore:
(36)
In which, when "p" tends to infinite
then "
" will tend to constant
"A".
If we use a multiplication like for
integer numbers with a simple calculation:
(37)
And great difference between relations (36) and (37) shows clearly the effect of "rarefaction" of prime numbers.
Finally, the last result about the value of function
is about the situation in which
"n" is equal to multiplication of prime numbers from
"1" to "p" and we write:
(38)
When we put symbol of "!" in parenthesis, it means that we don’t have the multiplication of all integer numbers smaller than "p". Here, we involve only the multiplication of "p" in all prime numbers smaller than it.
Relation (1) is equivalent with below relation:
(39)
Number 
for the
numbers smaller than "n" and coprime with "n",
is:
(40)
and according to relations (36) and (39):
(41)
It is clear that this number is very greater than the
number of prime numbers which are smaller than "n" shown
.
This remark is interesting because it is inverse for
little values of "p" and "n". For example,
for 
and
:
Between these 48 numbers, "1" is determinate and prime numbers 2,3,5,7 aren’t so. Therefore there will be 51 prime numbers, in other word, if we don’t consider the numbers divisible by 11 and 13:
And consider only the numbers up to 5, then 46 prime
number will remain. Vice versa, If 
1 and
, the number of
prime numbers
smaller than "n" will be 
although:
Between this numbers,
there are only 
numbers that are prime number.
12.3. Statistical investigation into the fundamental formula for "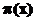
"
At first we consider relation (26):
(1)
This relation gives us the number of prime numbers in the
interval"
".
From the statistic results that are obtained from prime numbers tables, for all of numbers between 9 to 10 million, approximately:
(2)
In the other hand this value is "62082", therefore the error is equal to "148".
12.4. Separating intervals of prime numbers
Survey of intervals which separate two successive prime
numbers is an interesting sample of necessity of combining the probability
arithmetic rules with primary arithmetic. Beforehand we have mentioned
Poisson's rule that is about distribution of a lot of points on a very long
line. If we know the average concentration of points (the number of points on
unit of line) "
" (average concentration)
can be a fractional number smaller than unit.
If we suppose that the number of points on a line segment
with a length "x" is "n", then approximately "
" with a deviation equal to
.
Poisson’s relation determines (according to the function of "n") the probability of "k" points in a length "x", this probability is:
(1)
And also:
(2)
If we suppose that "O" is origin and
there is a point like "A" so that"
",
according to"", probability of existing
of no point on "
" is:
(3)
On other side, the probability of existing of a point in
an infinitely small distance "
" in the
right side of "A" is:
(4)
Multiplying the relations (3) and (4), we can calculate the probability that the nearest point to "O" is infinitely near to "A".
(It means that, this point is in distance "x"
and "
") this probability is:
(5)
The probability that point "A" (nearest point to "O") is between two point "B" and "C", with lengths "b" and "c" respectively, is:
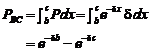(6)
Probability of being "A" between point "O" and point "C" is:
(7)
Average length of "OC" is:
(8)
If we suppose that "O" is one of the
points on the straight line, this result is obvious because according to
hypothesis, distance "OC" is "
".
But in our calculation, point "O" is not considered as an
arbitrary point. Now, if we consider "
"
as an arbitrary point in the left side of "O" and nearest
point to it (while "
" was in right side of
"O"), the average value of "
"
will also be "" so that average value of
"
" will be"
".
Probably, it seems paradoxical, because "" is an undetermined
distance that separate two adjacent points "C" and "" and we saw that the
average value of this distance was. The paradox
can be explained as follow:
If there are a lot of points, which indicate unequal
distances, on a line, average value of these distances is determinable by two
methods. The simple and natural method is that we choose big length of "x",
if there are "n" distances on this length, the average length
of every distance is"
". But we
can also use the below method.
We consider a random point like "
"
on the length of "x" and measure the distance that "" is on it. And we repeat
this action for a lot of points that are chosen randomly like
.
Then we calculate average value of distances of points
",
, … ,
". It is clear that new
method of calculation, determines the average value more than that of the
previous method. Because if we choose "," points, stochastically.
This chance is dominant than these points occur in greater distances, not on
the smaller distances.
In fact, the probability that a point settles on a distance with length "c" is proportional to "c", so that the average value can be calculated by the below relation instead of relation (8):
(9)
Because we know:
(10)
And in this way, the paradox has been completely clarified.
If instead of points chosen on straight conjoint line randomly, we choose them between points with integer coordination on the line, again we can use Poisson’s relation as an approximate relation.
1.
If for example 
and 
their
geometric average is 
and their arithmetic
average is 
Their difference isn’t more
than 
of their common value:
[1].
If we convert the series to integral, we must ignore the little term
.
1. It is better to say that "p" prime number is near to e100 completely, because e100 isn’t an integer number.