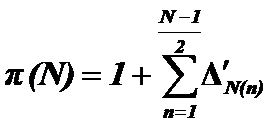CHAPTER 11
Decisive solution to determining "k-th" prime
number by determining function concerning the number of prime in a precise
manner
11.1. Determination of "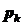
" in a precise manner
It has been proved that the number of prime numbers not more than "N", is exactly defined by the below relation:
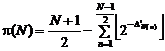(1)
If we consider "
" as kth prime
number, then it is obvious:
(2)
Therefore, If 
is equal to zero, then "N"
will be equal to the kth prime number"
". If expression
be non-zero, "N" will not be equal to kth prime
number. Now we consider the below expression:
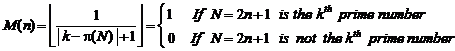
Here, we define 
with the below method:
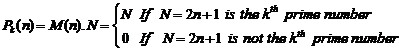(3)
It has been proved that the kth prime number is
smaller than
:
(4)
Therefore"
" (kth prime
number) is computable with the below relation
:
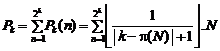(5)
Therefore, (kth prime number) is
defined as
:
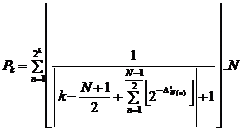(6)
11.1.1. Example
We calculate"
" with "" formula
(
):
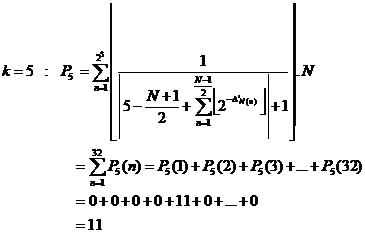
11.2. Other formulas for determining "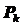
"in a precise manner
According to another formula for
, another formula for
""
can be presented as below (According to the primal conditions):
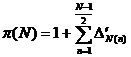(7)
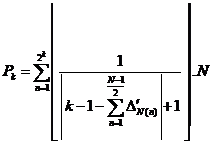(8)
11.2.1. Remark
For calculating "" it is possible use the
equation"
":
()
Therefore, we define the below simple expression:
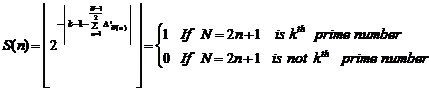
Here, we can define 
using
:
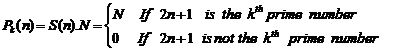(9)
Therefore, is computable by the below
relation:
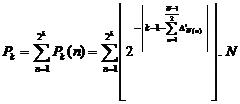(10)
So we can use every relations (5), (8) and (10) for
calculating"", but because of"
",
calculating "" may take too length and
time. To solve this problem, we can calculate instead of. It means that a
program can be written for calculating "
".
According to the condition 
and every mentioned relation for
and, we form the
below table:
|
|
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
23 |
… |
|
|
2 |
3 |
4 |
5 |
5 |
6 |
7 |
7 |
8 |
9 |
9 |
… |
|
|
3 |
5 |
7 |
0 |
11 |
13 |
0 |
17 |
19 |
0 |
23 |
… |
and also:
|
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
… |
|
|
3 |
5 |
7 |
11 |
13 |
17 |
19 |
23 |
29 |
31 |
37 |
41 |
43 |
… |
